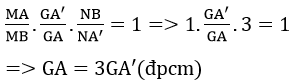Chứng minh rằng đường thẳng đi qua G và một đỉnh của tứ diện sẽ đi qua

Bài 2: Hai đường thẳng song song

Bài 22 (trang 55 sgk Hình học 11 nâng cao): Gọi C là trọng tâm của tứ diện ABCD.

a) Chứng minh rằng đường thẳng đi qua G và một đỉnh của tứ diện sẽ đi qua trọng tâm của mặt đối diện với đỉnh ấy.

b) Gọi A’ là trọng tâm của một BCD . Chứng minh rằng GA = 3GA’

Lời giải:

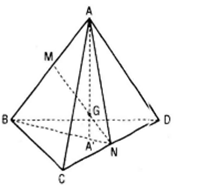
a) Trong mp(ABN) gọi A’ là giao điểm của AG với trung tuyến BN của ΔBCD . Ta chứng minh:

A’B = 2A’N

Áp dụng định lí Menelaus trong ΔBMN với cát tuyến AGA’ Ta có :

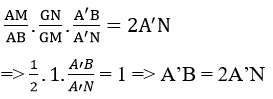
Vậy A’ là trọng tâm của Δ BCD

Tương tự BG, CG, DG lần lượt đi qua trọng tâm B’, C’, D’ của tam giác ACD, ABD, ABC

b) Chứng minh GA = 3GA’

Áp dụng định lí Menelaus trong ΔABA’ với cát tuyến MGN Ta có :