Chứng tỏ rằng hai hình bằng nhau

Bài 5: Hai hình bằng nhau

Bài 23 (trang 23 sgk Hình học 11 nâng cao): Hình H₁ gồm 3 đường tròn (O₁; r₁), ( O₂; r₂), ( O₃; r₃) đôi một tiếp xúc ngoài với nhau. Hình H₂ gồm ba đường tròn (I₁; r₁), ( I₂; r₂), ( I₃; r₃) đôi một tiếp xúc ngoài với nhau. Chứng tỏ rằng hai hình H₁ và H₂ bằng nhau.

Lời giải:

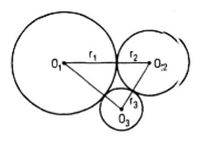
Ta có : O₁O₂ = r₁ + r₂ = I₁I₂

O₂O₃ = r₂ + r₃ = I₂I₃

O₃O₁ = r₃ + r₁ = I₃I₁

Suy ra ΔO₁O₂O₃= ΔI₁I₂I₃

Nên có phép dời hình F biến ba điểm O₁,O₂,O₃lần lượt ba điểm I₁,I₂,I₃. Hiển nhiên khi đo F biến ba đường tròn (O₁; r₁), ( O₂; r₂), ( O₃; r₃) lần lượng thành ba đường tròn (I₁; r₁), ( I₂; r₂), ( I₃; r₃) tức là biến hình H₁ thành hình H₂ . Vậy hai hình H₁ và H₂ bằng nhau