Cho đường tròn (O; R) và điểm I cố định khác O

Bài 6: Phép vị tự

Bài 29 (trang 29 sgk Hình học 11 nâng cao): Cho đường tròn (O; R) và điểm I cố định khác O. Một điểm M thay đổi trên đường tròn. Tia phân giác của góc MOI cắt IM tại N. Tìm quỹ tích điểm N.

Lời giải:

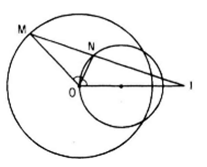
Đặt IO = d ( d ≠ 0). Theo tính chất đường phân giác của tam giác MOI, ta có :

IN/NM = IO/OM = d/R.

Suy ra :

IN/(IN + NM) = d/(d + R) ⇒ IN/IM = d/(d + R)

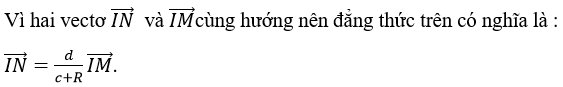
Nếu gọi V là phép vị tự tâm I tỉ số k = d/(d + R) thì V biến điểm M thành điểm N. Khi M ở vị trí M_o trên đường tròn (O; R) sao cho IÔM_o = 0_o thì tia phân giác của góc IÔM_o không cắt IM. Điểm N không tồn tại. Vậy khi M chạy trên (O; R) (M khác Mo) thì quỹ tích điểm N là ảnh của (O; R) qua phép vị tự V bỏ đi ảnh của điểm M_o.