Chứng minh rằng có đúng hai mặt phẳng song song với nhau

Bài 4: Hai mặt phẳng song song

Bài 31 (trang 68 sgk Hình học 11 nâng cao): Cho hai đường thẳng chéo nhau. Chứng minh rằng có đúng hai mặt phẳng song song với nhau lần lượt đi qua hai đường thẳng đó.

Lời giải:

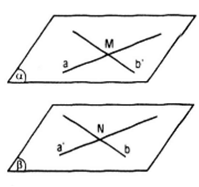
Gọi hai đường thẳng chéo nhau là a và b.

- Trên đường thẩng a ta lấy điểm M, qua M kẻ đường thẳng b’ // b.

- Trên đường thẳng b ta lấy điểm N, qua N ta kẻ đường thẳng a’ // a.

- Gọi (α) = mp(a, b’), (β) = mp(b, a’) thì (α) // (β) .

- Ta chứng tỏ cặp mp(α) , (β) là duy nhất . Thật vâỵ giả sử tồn tại cặp (α’) , (β’) sao cho (α’) chứa a, (β’) chứa b và (α’) // (β’). Ta chứng minh (α’) ≡ (α) và (β’) ≡ (β)

+ Do (α’) và (α) cùng chứa a, nên nếu (α’) và (α) không trùng nhau thì (α’) ∩ (α)= a (1)

+ Do (α’) // (β’) ⇒ b // (α) (2)

+ Do (α) // (β) ⇒ b // (α) (3)

Từ (1) , (2), (3) suy ra a // b mâu thuẫn giả thiết

Vậy (α’) ≡(α), tương tự (β’) ≡ (β)

Do đó cặp mp(α), (β) duy nhất.