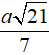Tính khoảng cách từ S đến mặt phẳng đáy (ABCD)

Bài 5: Khoảng cách

Bài 34 (trang 118 sgk Hình học 11 nâng cao): Cho hình chóp S.ABCD có đáy là hình chữ nhật và AB = 2a , BC = a. Các cạnh bên của hình chóp bằng nhau và bằng a√2

a) Tính khoảng cách từ S đến mặt phẳng đáy (ABCD)

b) Gọi E và F lần lượt là trung điểm của các canh AB và CD ; K là điểm bất kì thuộc đường thẳng AD. Chứng minh rằng khoảng cách giữa hai đường thẳng EF và SK không phụ thuộc vào k , hãy tính khoảng cách đó theo a.

Lời giải:

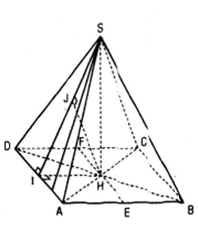
b) Vì EF // AD nên EF // mp(SAD), mặt khác SK nằm trong mp(SAD) nên khoảng cách giữa EF và SK chính là khoảng cách giữa EF và mp(SAD), đó cũng chính là khoảng cách từ H đến mp(SAD). Vậy khoảng cách giữa EF và SK không phụ thuộc vào vị trí của điểm K trên đường thẳng AD .

Tính d(EF; SK) :

Gọi I là trung điểm của AD , kẻ đường cao HJ của tam giác vuông SHI thì HJ ⊥ mp(SAD) do đó d(H; (SAD)) = HJ. Ta có : HJ. SI = SH. HI

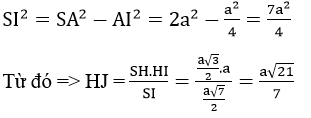
Như vậy khoảng cách giữa EF và SK không phụ thuộc vào vị trí của điểm K trên đường thẳng AD và bằng .