Cho tứ diện ABCD. Chứng minh rằng nếu AC = BD, AD = BC

Bài 5: Khoảng cách

Bài 35 (trang 118 sgk Hình học 11 nâng cao): Cho tứ diện ABCD. Chứng minh rằng nếu AC = BD, AD = BC thì đường vuông góc chung của AB và CD là đường thẳng nối trung điểm của AB và CD . Điều ngược lại có đúng k?

Lời giải:

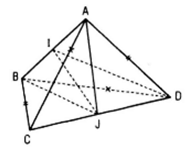
a) Vì AC = BD, AD = BC nên tam giác ACD bằng tam giác BDC, từ đó hai trung tuyến tương ứng AJ và BJ bằng nhau (ở đó J là trung điểm của CD).

Gọi I là trung điểm của AB thì ta có tam giác ABJ cân tại J có JI là đường trung tuyến nên đồng thời là đường cao: JI ⊥ AB.

Tương tự như trên ta cũng có JI ⊥ CD. Vậy IJ là đường vuông góc chung của AB và CD.

b) Điều ngược lại của kết luận nêu ra trong bài toán cũng đúng, tức là nếu IJ ⊥ AB, IJ ⊥ CD với I, J lần lượt là trung điểm của AB và CD thì AC = BD; AD = BC

Thật vậy vì IJ ⊥ AB , I là trung điểm của AB nên tam giác ABJ cân tại J, AJ = BJ.

Mặt khác, theo công thức độ dài đường trung tuyến của tam giác của tam giác ta có: