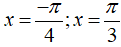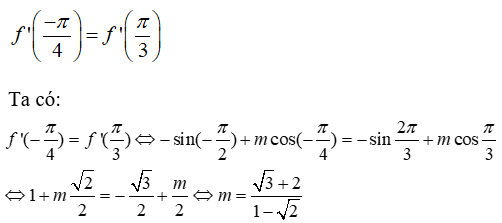Tiếp tuyến của (C) tại điểm với hoành độ x

Luyện tập trang 212-113

Bài 38 (trang 213 sgk Đại Số và Giải Tích 11 nâng cao): Cho hàm số y = cos²x + msinx (m là tham số) có đồ thị là (C) . Tìm m trong mỗi trường hợp sau :

a) Tiếp tuyến của (C) tại điểm với hoành độ x = π có hệ số góc bằng 1.

b) Hai tiếp tuyến của (C) tại các điểm có hoành độ x = -π/4 và x = π/3 song song với nhau hoặc trùng với nhau.

Lời giải:

Đặt f(x) = cos²x + msinx, ta có :

f’(x) = 2cosx.(-sinx) + mcosx = - sin2x + m.cosx

a) Hệ số góc tiếp tuyến của (C) tại điểm có hoành độ x = πlà :

f’(π) = -2sin2π + mcosπ = - 2. 0 + m.(-1) = - m

Vậy f’(π) = 1 ⇔ m = -1

b) Để tiếp tuyến của ( C) tại các điểm có hoành độ song song hoặc trùng với nhau thì hệ số góc của tiếp tuyến tại hai điểm đó bằng nhau- tức là: