Chứng minh rằng với mọi n: trang 219 sgk Đại Số và Giải Tích 11 nâng cao

Bài 5: Đạo hàm cấp cao

Bài 43 (trang 219 sgk Đại Số và Giải Tích 11 nâng cao): Chứng minh rằng với mọi n ≥ 1, ta có :

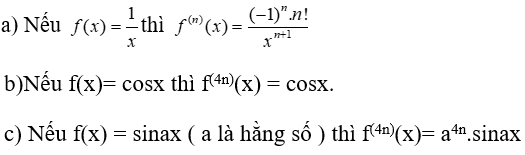
Lời giải:

b) Cho f(x) = cosx. Ta hãy chứng minh công thức:

f⁽⁴ⁿ⁾(x) = cosx (với n ≥ 1)

(2) bằng phương pháp quy nạp

Ta có: f(x) = -sinx; f’’(x) = -cosx; f’’’(x) = sinx; f⁽⁴⁾ (x) = cosx

+ Với n=1 thì f⁽⁴ⁿ⁾(x) = f⁽⁴⁾(x) = cosx

Suy ra (2) đúng khi n=1

+Giả sử (2) đúng cho trường hợp n=k (k ≥ 1 ),

tức là: f^(4k)(x) = cosx ,

Ta phải chứng minh (2) cũng đúng cho trường hợp n=k+1,

tức là phải chứng minh: f^{[4(k + 1)]}(x) = cosx (hay f^{(4k + 4)}(x) = cosx )

Thật vậy, vì : f^(4k)(x) = cosx nên f^{(4k + 1)}(x) = -sinx

f^{(4k + 2)}(x) = -cosx ; f^{(4k + 3)}(x) = sinx ;

f^{(4k + 4)}(x) = cosx

c) Ta có:f’(x) = acosax ; f’’(x) = -a².sinax

f⁽³⁾(x) = -a³cosax ; f⁽⁴⁾(x) = a⁴sinax

Với n=1 ta có f⁽⁴⁾(x) = a⁴sinax

đẳng thức đúng với n=1

Giả sử đẳng thức đúng với n=k tức là f^(4k)(x) = a^4ksinax

Ta chứng minh đúng với n = k + 1 tức là: f^[4(k+1)] (x) = a^4(k+1).sinax hay f^{(4k+ 4)} (x) = a^4(k+1).sin. Thật vậy,

f^{(4k + 1)}(x) = a^4k+1.cosax ;

f^{(4k + 2)}(x) = -a^4k+2.sinax ;

f^{(4k + 3)}(x) = -a^4k+3.cosax ;

f^{(4k + 4)} (x) = a^4k+4.sinax ;

Vậy đẳng thức đúng với n = k + 1, do đó đẳng thức đũng với mọi n.