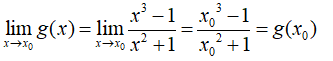Chứng minh rằng: trang 172 sgk Đại Số và Giải Tích 11 nâng cao

Bài 8: Hàm số liên tục

Bài 46 (trang 172 sgk Đại Số và Giải Tích 11 nâng cao): Chứng minh rằng:

Lời giải:

a) Hàm số f(x) = x³ - x + 3 xác định trên R. Với mọi x_o ∈ R, ta có:

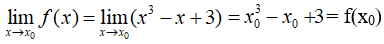
Vậy f liên tục tại điểm x_o.

Do đó hàm số f liên tục tại mọi điểm của R

+) Xét hàm số y = g(x)

Ta có: x² + 1 > 0 với mọi x nên hàm số y= g(x) xác định với mọi x.

Với ∀ x₀ ∈ R ta có:

Do đó, hàm số y = g(x) liên tục tại mọi điểm x ∈ R .

b) Với mọi x ≠ 2, ta có:

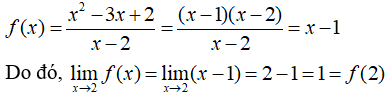
Vậy hàm số f liên tục tại điểm x = 2

c) Với mọi x ≠ 1, ta có:

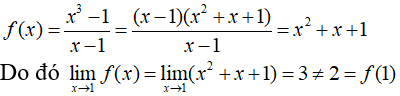
Vậy hàm số f gián đoạn tại điểm x = 1.