Giáo án Toán 9 Chương 4: Hàm số y = ax (a ≠ 0) - Phương trình bậc hai một ẩn mới nhất
Haylamdo biên soạn và sưu tầm Với mục đích giúp các Thầy / Cô giảng dạy môn Toán dễ dàng biên soạn Giáo án Toán lớp 9, VietJack biên soạn Bộ Giáo án Toán 9 Chương 4: Hàm số y = ax (a ≠ 0) - Phương trình bậc hai một ẩn phương pháp mới theo hướng phát triển năng lực bám sát mẫu Giáo án môn Toán chuẩn của Bộ Giáo dục. Hi vọng tài liệu Giáo án Toán 9 này sẽ được Thầy/Cô đón nhận và đóng góp những ý kiến quí báu.
Mục lục Giáo án Toán 9 Chương 4: Hàm số y = ax (a ≠ 0) - Phương trình bậc hai một ẩn
- Giáo án Toán 9 Bài 1: Hàm số y = ax2 (a ≠ 0)
- Giáo án Toán 9 Bài 2: Đồ thị hàm số y = ax2 (a ≠ 0)
- Giáo án Toán 9 Luyện tập trang 38-39
- Giáo án Toán 9 Bài 3: Phương trình bậc hai một ẩn
- Giáo án Toán 9 Bài 4: Công thức nghiệm của phương trình bậc hai
- Giáo án Toán 9 Bài 5: Công thức nghiệm thu gọn
- Giáo án Toán 9 Luyện tập trang 49-50
- Giáo án Toán 9 Bài 6: Hệ thức Vi-ét và ứng dụng
- Giáo án Toán 9 Luyện tập trang 54
- Giáo án Toán 9 Bài 7: Phương trình quy về phương trình bậc hai
- Giáo án Toán 9 Luyện tập trang 56-57
- Giáo án Toán 9 Bài 8: Giải bài toán bằng cách lập phương trình
- Giáo án Toán 9 Luyện tập trang 59-60
- Giáo án Toán 9 Ôn tập chương 4 Đại số
Giáo án Toán 9 Bài 1: Hàm số y = ax2 (a ≠ 0)
I. Mục tiêu:
Qua bài này HS cần:
1. Kiến thức:
- Thấy được trong thực tế có những hàm số dạng y=ax2(a 0).
- Phát biểu được tính chất của hàm số y=ax2(a 0).
- Liên hệ được ví dụ và ứng dụng thực tế của hàm.
2. Kĩ năng:
- Biết cách tính giá trị của hàm số tương ứng với giá trị cho trước của biến số.
- Tính được giá trị của hàm số tương ứng với giá trị cho trước của biến số.
3. Thái độ:
- Nghiêm túc và hứng thú học tập.
4. Định hướng năng lực, phẩm chất
- Năng lực tính toán, giải quyết vấn đề, hợp tác, giao tiếp, tự học.
Phẩm chất: Tự tin, tự chủ
II. Chuẩn bị:
- Gv : Phấn mầu, bảng phụ, thước thẳng
- Hs: Đồ dùng học tập, đọc trước bài.
III. Tiến trình dạy học:
1. Ổn định :(1 phút)
2. Bài mới :
| Giáo viên | Học sinh | Nội dung ghi bài | ||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Hoạt động 1: KHỞI ĐỘNG – 1p Như sách giáo khoa đặt vấn đề: giới thiệu về chương IV. HS thấy được sự cần thiết và tính tò mò phải đi tìm hiểu về một hàm số mới dạng y = ax2 (a ≠ 0) khác với hàm số bậc nhất một ẩn y = ax + b (a ≠ 0) đã được học. |
||||||||||||||||||||||||||||||||||
|
Hoạt động 2: HÌNH THÀNH KIẾN THỨC – 29p GV Tổ chức các HĐ để HS định hướng phát triển năng lực và phẩm chất cần có trong lúc hình thành được 3 đơn vị kiến thức mới: Công thức TQ hàm số y = ax2 (a ≠ 0); tính chất và nhận xét. Ví dụ mở đầu Mục tiêu: HS phát biểu được ví dụ mở đầu trong sgk, chỉ ra được sự tương ứng 1-1 giữa t và s, qua đó phát biểu được khái niệm hàm số y = ax2 (a ≠ 0) Kĩ thuật sử dụng: Động não, hoàn tất một nhiệm vụ, |
||||||||||||||||||||||||||||||||||
GV gọi một HS đọc ví dụ mở đầu. GV: Trong thực tế còn rất nhiều cặp đại lượng cũng được liên hệ với nhau bởi công thức có dạng y = ax2 (a ≠ 0), chẳng hạn diện tích hình vuông và cạnh của nó: S = a2, diện tích hình tròn và bán kính của nó S = πR2… GV: Hàm số y = ax2 (a ≠ 0) là dạng đơn giản nhất của hàm số bậc hai. Sau đây chúng ta xét các tính chất của hàm số đó. |
HS: Đọc bài HS quan sát trả lời HS trả lời HS nắm chắc công thức tổng quát của hàm số y = ax2 (a ≠ 0) |
1. Ví dụ mở đầu Xem SGK/28 |
||||||||||||||||||||||||||||||||
|
GV HD HS quan sát các bảng giá trị của hai hàm số cụ thể a > 0 ; a < 0 qua đó rút ra nhận xét và tổng quát nên thành tính chất của hàm số mới vừa học. 2/ Tính chất của hàm số y = ax2 (a ≠ 0) Bảng 1:
Bảng 2:
|
||||||||||||||||||||||||||||||||||
GV: Gọi HS nhận xét bài làm của các bạn. GV: Chỉ vào bảng số 1 và nêu câu hỏi của bài ?2 sgk. GV: Yêu cầu HS nhận xét tương tự đối với hàm số y = –2x2. GV: Nói một cách tổng quát, hàm số y = ax2 (a ≠ 0) xác định với mọi giá trị của x thuộc R và người ta chứng minh được nó có các tính chất sau: (GV đưa lên bảng phụ các tính chất của hàm số đó). |
HS nhận xét bài làm của các bạn. HS trả lời hai câu hỏi trong bài tập ?2 sgk. HS nhận xét tương tự đối với hàm số y = –2x2. |
*Đối với hàm số: y = 2x2 - Khi x<0; x tăng thì y giảm - Khi x>0; x tăng thì y tăng *Đối với hàm số: y = -2x2 - Khi x<0; x tăng thì y tăng - Khi x>0; x tăng thì y giảm * Tổng quát: - Nếu a>0 thì hàm số ĐB khi x>0; NB khi x<0 - Nếu a<0 thì hàm số ĐB khi x<0; NB khi x>0 |
||||||||||||||||||||||||||||||||
| GV yêu cầu HS hoạt động nhóm làm bài ?3 và cự đại diện một nhóm lên bảng trình bày bài làm. GV nêu phần nhận xét SGK |
HS nghe GV nêu tổng quát. HS đọc kết luận tổng quát. . . HS hoạt động nhóm làm bài ?3 và cử đại diện một nhóm lên bảng trình bày bài làm.s HS đại diện hai nhóm lên bảng điền vào ô trống |
?3: Đối với hàm số y=2x2, khi x 0 giá trị của y dương, khi x=0 thì y=0 Đối với hàm số y=2x2, khi x 0 giá trị của y âm, khi x=0 thì y=0 * Nhận xét: Với y = ax2 (a 0) - Nếu a>0 thì y>0 với mọi x ≠ 0; y=0 khi x=0. Giá trị nhỏ nhất của hàm số là y = 0 - Nếu a<0 thì y>0 với mọi x ≠ 0; y=0 khi x=0 thì giá trị lớn nhất của hàm số là y = 0 |
||||||||||||||||||||||||||||||||
|
Hoạt động 3, 4: LUYỆN TẬP, VẬN DỤNG – 8p Mục tiêu: Nhắc lại được tính chất của hàm số y = ax2 ( a 0 ), vận dụng kiến thức giải bài tập có liên quan. Kĩ thuật sử dụng: Hỏi và trả lời, hoàn tất một nhiệm vụ. Cho HS làm ?4/30 để củng cố lại tính chất và nhận xét trên GV đưa bảng phụ lên, yêu cầu hai HS đại diện hai nhóm lên bảng điền vào ô trống
HS1: Nhận xét: a = y = 0 khi x = 0. Giá trị nhỏ nhất của hàm số là y = 0. HS2: Nhận xét : a = – y = 0 khi x = 0. Giá trị lớn nhất của hàm số là y = 0. |
||||||||||||||||||||||||||||||||||
Hoạt động 5: TÌM TÒI, MỞ RỘNG – 6p Mục tiêu: Biết sử dụng máy tính để tính GTBT PP: Thực hành 1. Dùng máy tính CASIO để tính giá trị của một biểu thức • Ví dụ 1: Tính giá trị của biểu thức : A = 3x2 – 3,5x + 2 với x = 4,13 HS thực hiện tính bằng máy CASIO như SGK, tr32 • Ví dụ 2: Tính diện tích của một hình tròn có bkính R ( S = πR2 ) với R = 0,61; 1,53 ; 2,49 HS thực hiện tính bằng máy CASIO như SGK, tr32 2. Bài tập về nhà: số 2; 3 tr 31 SGK ; bài 1 , 2 tr 36 SBT. - GV: Hướng dẫn bài 3 SGK : Công thức F = av2 a) Tính a v = 2 m/s ; F = 120 N ; F = av2 => a = b) Tính F v1 = 10 m/s ; v2 = 20 m/s ; F = av2 |
||||||||||||||||||||||||||||||||||
Giáo án Toán 9 Bài 2: Đồ thị hàm số y = ax2 (a ≠ 0)
I. Mục tiêu:
Qua bài này HS cần:
1. Kiến thức:
- Mô tả được hình dạng của đồ thị hàm số y = ax2( a ≠ 0) và phân biệt được chúng trong hai trường hợp a > 0; a < 0.
- Phát biểu được tính chất của đồ thị và liên hệ được tính chất của đồ thị với tính chất của hàm số y = ax2( a ≠ 0 ).
- Làm được bài tập có liên quan.
2. Kĩ năng:
- Vẽ chính xác đồ thị hàm số y = ax2 (a ≠ 0)
3. Thái độ:
- Nghiêm túc và hứng thú học tập.
4. Định hướng năng lực, phẩm chất
- Năng lực tính toán, giải quyết vấn đề, hợp tác, giao tiếp, tự học.
Phẩm chất: Tự tin, tự chủ
II. Chuẩn bị:
- Gv : Phấn mầu, bảng phụ, thước thẳng, PHT
- Hs: Đồ dùng học tập, đọc trước bài.
III. Tiến trình dạy học:
1.Ổn định :(1 phút)
2.Kiểm tra bài cũ : (3p) Nêu t/c của hàm số y=ax2 (a ≠ 0)
3.Bài mới :
| Giáo viên | Học sinh | Nội dung ghi bài | ||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Hoạt động 1: Khởi động – 4p Điền vào ô trống các giá trị tương ứng của bảng sau
Trên mặt phẳng tọa độ, đồ thị của hàm số y=f(x) là tập hợp các điểm M(x;f(x)). Để xác định 1 điểm của đồ thị ta lấy 1 giá trị của x làm hoành độ còn tung độ là giá trị tương ứng của y=f(x). Ta đã biết đồ thị hàm số y = ax + b (a ≠ 0) là 1 đường thẳng, vậy đồ thị hàm số y=ax2 (a ≠ 0) có dạng như thế nào ta vào bài mới. |
||||||||||||||||||||||||||||||||||
Hoạt động 2: Hình thành kiến thức – 27p Mục tiêu: HS biết vẽ đồ thị hàm số PP: Vấn đáp, thuyết trình, hoạt động nhóm |
||||||||||||||||||||||||||||||||||
Gv giới thiệu cách vẽ như sgk Gv đưa hệ tọa độ đã vẽ sẵn các điểm ở bảng phụ. Gv nối các điểm bởi các cung. Yêu cầu hs trả lời các câu hỏi ở ?1 ? Em có nhận xét gì về dạng của đồ thị - Gv giới thiệu: Đồ thị này được gọi là 1 parabol, điểm O(0,0) gọi là đỉnh của parabol. Trường hợp này điểm O gọi là điểm thấp nhất của đồ thị. - Gv treo bảng phụ vẽ sẵn Cho Hs tiến hành như ví dụ 1 Gv giới thiệu nhận xét tổng quát Cho HS làm tiếp ?3 Gv hướng dẫn: a, Muốn tìm một điểm trên đồ thị có hoành độ x0, ta chỉ việc kẻ đường thẳng đi qua điểm biểu diễn x0 trên trục Ox và //Oy, cắt đồ thị tại 1 điểm. Đó là điểm cần tìm. b, Tương tự, lưu ý rằng đường thẳng song song với Ox nếu cắt đồ thị thì phải cắt ở hai điểm đối xứng nhau qua trục Oy, vì đồ thị nhận Oy làm trục đối xứng. GV nêu chú ý khi vẽ đồ thị hàm số y=ax2 (a ≠ 0) Gv thực hành mẫu bằng cách vẽ đồ thị hàm số y= |
HS hoạt động cá nhân HS vẽ đồ thị của hàm số y=2x2 HS làm ?1 HS đứng tại chỗ trả lời ?1 HS tiến hành như ví dụ 1 Hs vẽ đồ thị hàm số y= - Hs hoạt động nhóm làm ?3 HS sử dụng đồ thị ở ví dụ 2 để làm ?3 HS đứng tại chỗ trả lời. HS đọc chú ý SGK. |
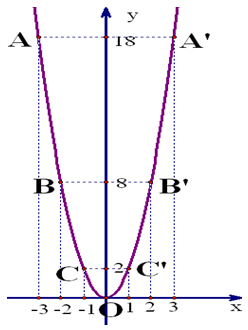
Ví dụ 1: Đồ thị hàm số y=2x2
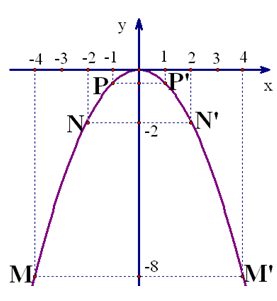
– Đồ thị của hàm số nằm phía trên trục hoành – Vị trí của các cặp điểm A và A’, B và B’, C và C’ đối xứng với nhau qua trục Oy – Điểm O(0;0) là điểm thấp nhất của đồ thị Ví dụ 2: Đồ thị hàm số y = -
– Đồ thị của hàm số nằm phía dưới trục hoành – Vị trí của các cặp điểm M và M’, N và N’, P và P’ đối xứng với nhau qua trục Oy – Điểm O(0;0) là điểm cao nhất của đồ thị Nhận xét: Xem SGK/35 ?3/35 a/ Qua điểm (3;0) vẽ đường thẳng // với Oy cắt đồ thị tại D(3; 4,5) b/ Qua điểm (0; 5) vẽ đường thẳng // Ox cắt đồ thị tại hai điểm * Chú ý: em SGK/35 |
||||||||||||||||||||||||||||||||
|
Hoạt động 3,4: Luyện tập, vận dụng – 8p Gv: Yêu cầu hs thảo luận làm bài tập 4 – SGK ( 1 nửa lớp thảo luận vẽ đồ thị hs Hs: Thảo luận làm bài |
||||||||||||||||||||||||||||||||||
Hoạt động 5: Tìm tòi, mở rộng – 2p + Bài tập về nhà: 4/ 36, 5/37 6/38 SGK + Đọc phần có thể em chưa biết SGK/36 và bài đọc thêm SGK/37,38 |
||||||||||||||||||||||||||||||||||



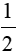 > 0 nên y > 0 với mọi x ≠ 0;
> 0 nên y > 0 với mọi x ≠ 0;
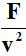
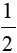 x2
x2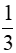 x2
x2
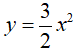 , một nửa lớp thảo luận vẽ đồ thị hs
, một nửa lớp thảo luận vẽ đồ thị hs 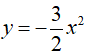 )
)