Tính khoảng cách từ một điểm đến một đường thẳng trong các trường hợp sau a) A(- 3; 1) và ∆1 2x + y – 4 = 0
Tính khoảng cách từ một điểm đến một đường thẳng trong các trường hợp sau:
Giải sách bài tập Toán 10 Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng
Bài 42 trang 82 SBT Toán 10 Tập 2: Tính khoảng cách từ một điểm đến một đường thẳng trong các trường hợp sau:
a) A(- 3; 1) và ∆1: 2x + y – 4 = 0;
b) B(1; - 3) và 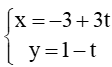
Lời giải:
a) Ta có: vectơ pháp tuyến của đường thẳng là =(2;1)
Suy ra d(A,)= 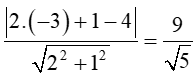
b) có vectơ chỉ phương là =(3;-1) và đi qua điểm A(-3; 1).
Vectơ pháp tuyến của đường thẳng là: =(1;3).
Suy ra phương trình đường thẳng là: x + 3 + 3( y – 1) = 0 hay x + 3y = 0
d(B,)= 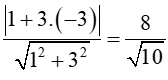

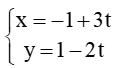 ? ....
? ....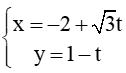 và :
và :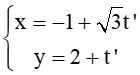 . Số đo góc giữa hai đường thẳng ∆1 và ∆2 là ....
. Số đo góc giữa hai đường thẳng ∆1 và ∆2 là ....