Cho hai đường thẳng song song ∆1: ax + by + c = 0 và ∆2: ax + by + d = 0
Cho hai đường thẳng song song ∆: ax + by + c = 0 và ∆: ax + by + d = 0. Chứng minh rằng khoảng cách giữa hai đường thẳng ∆ và ∆ bằng .
Giải sách bài tập Toán 10 Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng
Bài 43 trang 82 SBT Toán 10 Tập 2: Cho hai đường thẳng song song ∆1: ax + by + c = 0 và ∆2: ax + by + d = 0. Chứng minh rằng khoảng cách giữa hai đường thẳng ∆1 và ∆2 bằng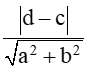 
.
Lời giải:
Gọi M(x0;y0) thuộc ∆1 nên ax0+by0+c=0.
Khoảng cách giữa ∆1 đến ∆2 bằng khoảng cách từ M đến ∆2 bằng
d(M;∆2)=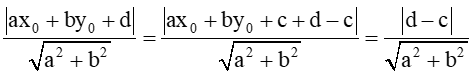
.
Vậy bài toán được chứng minh.
? ....
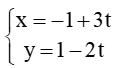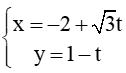và :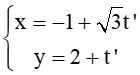
. Số đo góc giữa hai đường thẳng ∆1 và ∆2 là ....