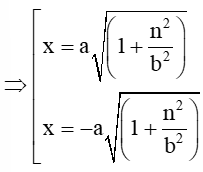Cho hypebol (H) có phương trình chính tắc x^2/a^2+y^2/b^2=1 với a > 0, b > 0 và đường thẳng y = n

Cho hypebol (H) có phương trình chính tắc: =1 với a > 0, b > 0 và đường thẳng y = n cắt (H) tại hai điểm P, Q phân biệt. Chứng minh hai điểm P và Q đối xứng nhau qua trục Oy.

Giải sách bài tập Toán 10 Bài 6: Ba đường conic

Bài 68 trang 97 SBT Toán 10 Tập 2: Cho hypebol (H) có phương trình chính tắc: $\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1 với a > 0, b > 0 và đường thẳng y = n cắt (H) tại hai điểm P, Q phân biệt. Chứng minh hai điểm P và Q đối xứng nhau qua trục Oy.

Lời giải:

Thay y = n vào phương trình chính tắc của Parabol ta có: $\frac{x^2}{a^2}-\frac{n^2}{b^2}$=1

Suy ra x²=a².$\left(1+\frac{n^2}{b^2}\right)$

Giả sử điểm P$\left(a\sqrt{\left(1+\frac{n^2}{b^2}\right)};n\right)$ và Q$\left(-a\sqrt{\left(1+\frac{n^2}{b^2}\right)};n\right)$

Do Q và P có cùng tung độ và hoành độ đối nhau nên P và Q đối xứng nhau qua trục Oy