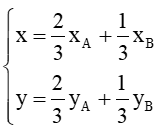Trong mặt phẳng toạ độ Oxy, cho hai điểm A(3; 4), B(8; 6). Kẻ đường phân giác trong OD

Trong mặt phẳng toạ độ Oxy, cho hai điểm A(3; 4), B(8; 6). Kẻ đường phân giác trong OD của tam giác OAB (D thuộc đoạn AB).

Sách bài tập Toán 10 Kết nối tri thức Bài tập ôn tập cuối năm

Bài 12 trang 72 Sách bài tập Toán lớp 10 Tập 2: Trong mặt phẳng toạ độ Oxy, cho hai điểm A(3; 4), B(8; 6). Kẻ đường phân giác trong OD của tam giác OAB (D thuộc đoạn AB).

a) Tính OA, OB.

b) Chứng minh rằng $\overrightarrow{OD}=\frac{2}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$.

c) Tìm toạ độ điểm D.

Lời giải:

a) Ta có: A(3; 4), suy ra $\overrightarrow{OA}=\left(3;4\right)$, do đó OA = $\sqrt{3^2+4^2}=5$.

B(8; 6), suy ra $\overrightarrow{OB}=\left(8;6\right)$, do đó OB = $\sqrt{8^2+6^2}=10$.

b) Do OD là đường phân giác trong của tam giác OAB nên theo tính chất đường phân giác ta có: $\frac{AD}{BD}=\frac{OA}{OB}=\frac{5}{10}=\frac{1}{2}$.

Suy ra: BD = 2AD.

Mặt khác do D thuộc đoạn AB nên hai vectơ $\overrightarrow{AD},\overrightarrow{BD}$ ngược hướng.

Do vậy, $\overrightarrow{BD}=-2\overrightarrow{AD}$.

Mà $\overrightarrow{BD}=\overrightarrow{OD}-\overrightarrow{OB};\overrightarrow{AD}=\overrightarrow{OD}-\overrightarrow{OA}$

Từ đó ta có: $\overrightarrow{OD}-\overrightarrow{OB}=-2(\overrightarrow{OD}-\overrightarrow{OA})$

$\iff 3\overrightarrow{OD}=2\overrightarrow{OA}+\overrightarrow{OB}$

$\iff \overrightarrow{OD}=\frac{2}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$ (đpcm).

c) Gọi D(x; y), do $\overrightarrow{OD}=\frac{2}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$, suy ra:

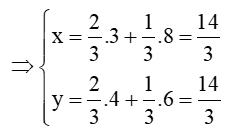
Vậy $D\left(\frac{14}{3};\frac{14}{3}\right)$.