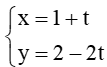Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có M, N, P lần lượt là trung điểm

Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có M, N, P lần lượt là trung điểm của các đoạn thẳng BC, AC, AB. Biết rằng M(1; 2), N(0; –1) và P(–2; 3).

Sách bài tập Toán 10 Kết nối tri thức Bài tập ôn tập cuối năm

Bài 13 trang 72 Sách bài tập Toán lớp 10 Tập 2: Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có M, N, P lần lượt là trung điểm của các đoạn thẳng BC, AC, AB. Biết rằng M(1; 2), N(0; –1) và P(–2; 3).

a) Lập phương trình tham số của đường thẳng BC.

b) Lập phương trình tổng quát của đường trung trực của đoạn thẳng BC.

Lời giải:

a) Do P và N lần lượt là trung điểm của AB và AC nên PN là đường trung bình của tam giác ABC, do đó PN // BC.

Ta có: $\overrightarrow{PN}=\left(2;-4\right)$

Do đó, một vectơ chỉ phương của đường thẳng BC là $\overrightarrow{u_{BC}}=\frac{1}{2}\overrightarrow{PN}=\frac{1}{2}\left(2;-4\right)=\left(1;-2\right)$.

Mặt khác đường thẳng BC đi qua điểm M(1; 2) (do M là trung điểm của BC).

Vậy phương trình tham số của đường thẳng BC là:

b) Gọi d là đường trung trực của đoạn thẳng BC.

Ta có d đi qua trung điểm M của BC và vuông góc với BC.

Do đó, $\overrightarrow{n_d}=\overrightarrow{u_{BC}}=\left(1;-2\right)$ là vectơ pháp tuyến của đường thẳng d.

Vậy phương trình tổng quát của đường thẳng d là:

1(x – 1) – 2(y – 2) = 0 hay x – 2y + 3 = 0.