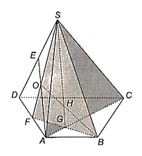
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi O là một điểm nằm trong tam giác SAD

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi O là một điểm nằm trong tam giác SAD.

Giải sách bài tập Toán 11 Bài tập cuối chương 4 - Kết nối tri thức

Bài 4.60 trang 73 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi O là một điểm nằm trong tam giác SAD.

a) Xác định giao điểm của đường thẳng AO và mặt phẳng (SCD).

b) Xác định giao tuyến của hai mặt phẳng (SBO) và (SAC).

c) Xác định giao điểm của đường thẳng BO và mặt phẳng (SAC).

Lời giải:

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi O là một điểm nằm trong tam giác SAD

a) Trong mặt phẳng (SAD) gọi E là giao điểm của AO và SD thì E là giao điểm của AO và mặt phẳng (SCD).

b) Trong mặt phẳng (SAD) gọi F là giao điểm của SO và AD.

Trong hình thang ABCD, đường thẳng AC cắt BF tại G.

Ta có G ∈ AC ⊂ (SAC) và G ∈ BF ⊂ (SBO) nên G là một điểm chung của hai mặt phẳng (SBO) và (SAC).

Lại có S cũng là một điểm chung của hai mặt phẳng (SBO) và (SAC).

Vậy SG là giao tuyến của hai mặt phẳng (SBO) và (SAC).

c) Trong mặt phẳng (SBO) gọi H là giao điểm của BO và SG.

Do G thuộc mặt phẳng (SAC) nên đường thẳng SG nằm trong mặt phẳng (SAC).

Vậy H là giao điểm của đường thẳng BO và mặt phẳng (SAC).

Lời giải SBT Toán 11 Bài tập cuối chương 4 hay khác: