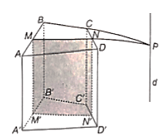
Cho hình lăng trụ tứ giác ABCD.A'B'C'D'. Gọi M, N, M', N' lần lượt là trung điểm của các cạnh AB, CD, A'B', C'D'

Cho hình lăng trụ tứ giác ABCD.A'B'C'D'. Gọi M, N, M', N' lần lượt là trung điểm của các cạnh AB, CD, A'B', C'D'.

Giải sách bài tập Toán 11 Bài tập cuối chương 4 - Kết nối tri thức

Bài 4.61 trang 74 SBT Toán 11 Tập 1: Cho hình lăng trụ tứ giác ABCD.A'B'C'D'. Gọi M, N, M', N' lần lượt là trung điểm của các cạnh AB, CD, A'B', C'D'.

a) Chứng minh rằng bốn điểm M, N, M', N' đồng phẳng và tứ giác MNN'M' là hình bình hành.

b) Giả sử MN không song song với BC. Xác định giao tuyến của hai mặt phẳng (MNN'M') và (BCC'B').

Lời giải:

Cho hình lăng trụ tứ giác ABCD.A'B'C'D'. Gọi M, N, M', N' lần lượt là trung điểm của các cạnh AB, CD, A'B', C'D'

a) Vì M, M' lần lượt là trung điểm của hai cạnh AB, A'B' của hình bình hành ABB'A' nên MM' // AA' và MM' = AA'.

Tương tự NN' // DD' và NN' = DD'.

Tứ giác ADD'A' là hình bình hành nên AA' // DD' và AA' = DD'.

Vì vậy MM' // NN' và MM' = NN', suy ra bốn điểm M, N, M', N' đồng phẳng và tứ giác MNN'M' là hình bình hành.

b) Trong mặt phẳng (ABCD) gọi P là giao điểm của hai đường thẳng MN và BC.

Vì hai mặt phẳng (MNN'M') và (BCC'B') lần lượt chứa hai đường thẳng MM' và BB' song song với nhau nên giao tuyến của hai mặt phẳng (MNN'M') và (BCC'B') là đường thẳng d đi qua P và song song với BB'.

Lời giải SBT Toán 11 Bài tập cuối chương 4 hay khác:

Xem thêm lời giải Sách bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯