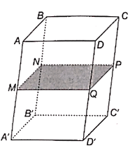
Cho hình hộp ABCD.A'B'C'D'. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AA', BB', CC', DD'
Cho hình hộp ABCD.A'B'C'D'. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AA', BB', CC', DD'. Chứng minh rằng bốn điểm M, N, P, Q đồng phẳng và MNPQ là hình bình hành.
Giải sách bài tập Toán 11 Bài tập cuối chương 4 - Kết nối tri thức
Bài 4.62 trang 74 SBT Toán 11 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AA', BB', CC', DD'. Chứng minh rằng bốn điểm M, N, P, Q đồng phẳng và MNPQ là hình bình hành.
Lời giải:
Vì M, N lần lượt là trung điểm của hai cạnh AA', BB' của hình bình hành ABB'A' nên ta có MN // AB, suy ra MN // (ABCD).
Tương tự NP // (ABCD), do đó (MNP) // (ABCD).
Lập luận tương tự suy ra (NPQ) // (ABCD).
Qua điểm N có hai mặt phẳng (MNP) và (NPQ) cùng song song với mặt phẳng (ABCD) nên hai mặt phẳng (MNP) và (NPQ) trùng nhau, tức là bốn điểm M, N, P, Q đồng phẳng.
Ngoài ra từ M, N lần lượt là trung điểm của hai cạnh AA', BB' của hình bình hành ABB'A' ta suy ra được MN = AB.
Do đó, MN // AB và MN = AB.
Tương tự, ta chứng minh được PQ // CD và PQ = CD.
Mà AB // CD và AB = CD (do ABCD là hình bình hành).
Khi đó, MN // PQ và MN = PQ nên tứ giác MNPQ là hình bình hành.
Lời giải SBT Toán 11 Bài tập cuối chương 4 hay khác:
Bài 4.48 trang 72 SBT Toán 11 Tập 1: Trong không gian cho hai đường thẳng cắt nhau a và b ....
Bài 4.50 trang 72 SBT Toán 11 Tập 1: Nếu mặt phẳng (R) cắt hai mặt phẳng song song (P) và (Q) ....
Bài 4.51 trang 72 SBT Toán 11 Tập 1: Cho ba mặt phẳng (P), (Q), (R) đôi một song song với nhau ....
Bài 4.52 trang 72 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD) ....
Bài 4.55 trang 73 SBT Toán 11 Tập 1: Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến d ....