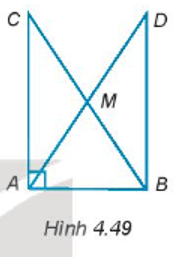
Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia đối của tia MA sao cho MD = MA (H.4.49)
Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia đối của tia MA sao cho MD = MA (H.4.49). Chứng minh rằng:
Giải SBT Toán 7 Kết nối tri thức Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng
Bài 4.44 trang 69 sách bài tập Toán lớp 7 Tập 1: Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia đối của tia MA sao cho MD = MA (H.4.49). Chứng minh rằng:
a) ∆ABD vuông tại B.
b) ∆ABD = ∆BAC.
c) Các tam giác AMB, AMC là các tam giác cân tại đỉnh M.
Lời giải:
a) Xét tam giác AMC và tam giác DMB có:
MA = MD (gt)
MB = MC (M là trung điểm của BC)
(hai góc đối đỉnh)
Do đó, ∆AMC = ∆DMB (c – g – c).
Suy ra (hai góc tương ứng).
Do tam giác ABC vuông tại A nên .
Khi đó, ta có: .
Suy ra .
Vậy tam giác ABD vuông tại B.
b) Xét tam giác vuông ABD và tam giác vuông BAC có:
BD = AC (do ∆AMC = ∆DMB)
AB: cạnh chung
Do đó, ∆ABD = ∆BAC (hai cạnh góc vuông).
c) Do tam giác ABC vuông tại A nên AC ⊥ AB tại A.
Tam giác ABD vuông tại B nên DB ⊥ AB tại B.
Suy ra AC // DB (do cùng vuông góc với AB).
(hai góc so le trong).
Lại có: (do ∆ABD = ∆BAC).
Do đó, , hay .
Suy ra tam giác AMC cân tại đỉnh M.
Khi đó MA = MC.
Mà MB = MC (do M là trung điểm của BC).
Nên MA = MB = MC.
Do đó, tam giác AMB cân tại đỉnh M.