Cho các điểm A, B, C, D, E như Hình 4.51. Chứng minh rằng

Cho các điểm A, B, C, D, E như Hình 4.51. Chứng minh rằng:

Giải SBT Toán 7 Kết nối tri thức Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng

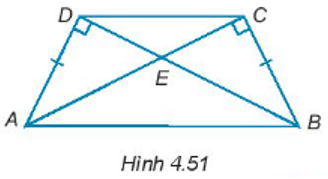
Bài 4.46 trang 69 sách bài tập Toán lớp 7 Tập 1: Cho các điểm A, B, C, D, E như Hình 4.51. Chứng minh rằng:

a) ∆AEB và ∆DEC là các tam giác cân đỉnh E.

b) AB // CD.

Cho các điểm A, B, C, D, E như Hình 4.51. Chứng minh rằng

Lời giải:

a) Xét tam giác vuông ADB và tam giác vuông BCA có:

AB: cạnh huyền chung

AD = CB (gt)

Do đó, ∆ADB = ∆BCA (cạnh huyền – cạnh góc vuông).

Suy ra $\hat{D B A} = \hat{C A B}$ , hay $\hat{E B A} = \hat{E A B}$ .

Khi đó tam giác EAB cân tại đỉnh E.

Xét tam giác vuông ADE và tam giác vuông BCE có:

AD = CB (gt)

EA = EB (∆EAB cân tại đỉnh E)

Do đó, ∆ADE = ∆BCE (cạnh huyền – cạnh góc vuông).

Suy ra ED = EC.

Do đó, tam giác EDC cân tại đỉnh E.

b) Theo định lí tổng 3 góc trong tam giác EAB, ta có:

$\hat{E B A} + \hat{E A B} + \hat{A E B} = 180 °$

Mà $\hat{E B A} = \hat{E A B}$ (chứng minh trên)

Suy ra $\hat{E B A} = \frac{180 ° - \hat{A E B}}{2}$ . (1)

Theo định lí tổng 3 góc trong tam giác EDC, ta có:

$\hat{E D C} = \hat{E C D} + \hat{D E C} = 180 °$

Mà $\hat{E D C} = \hat{E C D}$ (∆ECD cân tại đỉnh E).

Suy ra $\hat{E D C} = \frac{180 ° - \hat{D E C}}{2}$ . (2)

Ta lại có: $\hat{A E B} = \hat{D E C}$ (hai góc đối đỉnh). (3)

Từ (1), (2) và (3) suy ra $\hat{E B A} = \hat{E D C}$ , hay $\hat{D B A} = \hat{B D C}$ .

Mà hai góc này ở vị trí so le trong.

Vậy AB // DC.