Cho tam giác ABC cân tại đỉnh A có đường cao AH
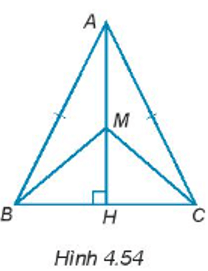
Cho tam giác ABC cân tại đỉnh A có đường cao AH. Cho M là một điểm tùy ý trên đường thẳng AH sao cho M không trùng với A (H.4.54).
Giải SBT Toán 7 Kết nối tri thức Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng
Bài 4.50 trang 70 sách bài tập Toán lớp 7 Tập 1: Cho tam giác ABC cân tại đỉnh A có đường cao AH. Cho M là một điểm tùy ý trên đường thẳng AH sao cho M không trùng với A (H.4.54).
Chứng minh rằng: ^MBA=^MCA.
Lời giải:
Xét tam giác vuông ABH và tam giác vuông ACH có:
AB = AC (∆ABC cân tại đỉnh A)
AH: cạnh chung
Do đó, ∆ABH = ∆ACH (cạnh huyền – cạnh góc vuông).
Suy ra ^BAH=^CAH, hay ^BAM=^CAM.
Xét tam giác ABM và ACM có:
AB = AC (∆ABC cân tại đỉnh A)
^BAM=^CAM
AM: cạnh chung
Do đó, ∆ABM = ∆ACM (c – g – c).
Suy ra ^MBA=^MCA.
