Ở một gian hàng của siêu thị người ta xếp các khối hàng hình lập phương

❮ Bài trước Bài sau ❯

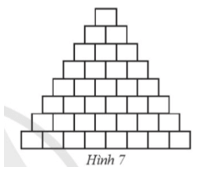
Ở một gian hàng của siêu thị, người ta xếp các khối hàng hình lập phương giống nhau thành hình tháp n tầng, với tầng đáy thứ n có n khối hàng, tầng ngay trên tầng đáy có (n – 1) khối hàng, ..., tầng trên cùng có 1 khối hàng (chẳng hạn với n = 8 ta có cách xếp như minh hoạ ở Hình 7).

Giải SBT Toán 9 Bài 2: Phương trình bậc hai một ẩn - Cánh diều

Bài 15 trang 65 SBT Toán 9 Tập 2: Ở một gian hàng của siêu thị, người ta xếp các khối hàng hình lập phương giống nhau thành hình tháp n tầng, với tầng đáy thứ n có n khối hàng, tầng ngay trên tầng đáy có (n – 1) khối hàng, ..., tầng trên cùng có 1 khối hàng (chẳng hạn với n = 8 ta có cách xếp như minh hoạ ở Hình 7).

Ở một gian hàng của siêu thị người ta xếp các khối hàng hình lập phương

a) Tính tổng số S các khối hàng đã xếp ở một hình tháp n tầng.

b) Tìm n, biết S = 120.

Lời giải:

a) Tổng số S các khối hàng ở một hình tháp n tầng là:

S=1+2+3+…+n−1+n=n+1⋅n2 (khối hàng).

b) Ta có: S=120, suy ra: n+1⋅n2=120 hay n2+n–240=0.

Phương trình n2+n–240=0 có ∆ = 12 ‒ 4.1.(‒240) = 961 > 0 và Δ=961=31.

Do đó, phương trình trên có hai nghiệm phân biệt là

n1=−1+312⋅1=302=15 (thoả mãn);

n2=−1−312⋅1=−322=−16 (không thoả mãn).

Vậy n = 15.

Lời giải SBT Toán 9 Bài 2: Phương trình bậc hai một ẩn hay khác:

Xem thêm các bài giải sách bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯
2018 © All Rights Reserved.