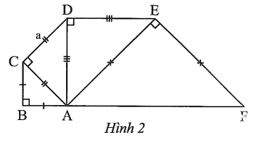
Một phần khung của một cây cầu gồm các thanh thép tạo thành các tam giác vuông cân như Hình 2

Một phần khung của một cây cầu gồm các thanh thép tạo thành các tam giác vuông cân như Hình 2. Biết rằng cạnh CD có độ dài a (m). Tính độ dài của đoạn BF theo a.

Giải sách bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

Bài 8 trang 51 sách bài tập Toán 9 Tập 1: Một phần khung của một cây cầu gồm các thanh thép tạo thành các tam giác vuông cân như Hình 2. Biết rằng cạnh CD có độ dài a (m). Tính độ dài của đoạn BF theo a.

Lời giải:

Do ∆ABC cân tại B nên BA = BC.

Do ∆ACD cân tại C nên CA = CD.

Do ∆ADE cân tại D nên DA = DE.

Do ∆AEF cân tại E nên EA = EF.

Xét ∆ACD vuông tại C, theo định lí Pythagore, ta có:

$DA=\sqrt{C{A}^2+C{D}^2}=\sqrt{2C{D}^2}=CD\sqrt{2}=a\sqrt{2}$(m).

Xét ∆ADE vuông tại D, theo định lí Pythagore, ta có:

$EA=\sqrt{D{A}^2{\text{+DE}}^2}=\sqrt{2D{A}^2}=DA\sqrt{2}=a\sqrt{2}\cdot \sqrt{2}=2a$ (m).

Xét ∆AEF vuông tại E, theo định lí Pythagore, ta có:

$AF=\sqrt{E{A}^2{\text{+EF}}^2}=\sqrt{2E{A}^2}=EA\sqrt{2}=2a\cdot \sqrt{2}=2a\sqrt{2}$(m).

Xét ∆ABC vuông tại B, theo định lí Pythagore, ta có:

$CA=\sqrt{B{A}^2+B{C}^2}=\sqrt{2B{A}^2}=BA\sqrt{2}$

Suy ra $BA=\frac{CA}{\sqrt{2}}=\frac{CD}{\sqrt{2}}=\frac{a}{\sqrt{2}}=\frac{a\sqrt{2}}{2}$(m).

Từ đó, $BF=BA+AF=\frac{a\sqrt{2}}{2}+2a\sqrt{2}=\frac{a\sqrt{2}}{2}+\frac{4a\sqrt{2}}{2}=\frac{5a\sqrt{2}}{2}$

Vậy $BF=\frac{5a\sqrt{2}}{2}\text{ (m).}$

Lời giải SBT Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay khác:

• Bài 1 trang 50 sách bài tập Toán 9 Tập 1: Trục căn thức ở mẫu các biểu thức: $\frac{5\sqrt{2}}{\sqrt{15}};$ ...

• Bài 2 trang 50 sách bài tập Toán 9 Tập 1: Khử mẫu của biểu thức lấy căn: $\sqrt{\frac{10}{11}};$ ...

• Bài 3 trang 50 sách bài tập Toán 9 Tập 1: Trục căn thức ở mẫu các biểu thức sau: $\frac{\sqrt{6}+2}{\sqrt{6}-2};$ ...

• Bài 4 trang 51 sách bài tập Toán 9 Tập 1: Cho hình hộp chữ nhật với chiều dài $3\sqrt{5}$ cm, chiều rộng $\sqrt{5}$ cm và thể tích $30\sqrt{5}$ cm³ như Hình 1. Tính tổng độ dài các cạnh của hình hộp chữ nhật đó ...

• Bài 5 trang 51 sách bài tập Toán 9 Tập 1: Rút gọn các biểu thức: $\sqrt{8}\cdot \sqrt{18}:\frac{\sqrt{5}}{\sqrt{2}};$ ...

• Bài 6 trang 51 sách bài tập Toán 9 Tập 1: Rút gọn các biểu thức: $4\sqrt{24}+\sqrt{6}-2\sqrt{54};$ ...

• Bài 7 trang 51 sách bài tập Toán 9 Tập 1: Rút gọn các biểu thức (biết a > 0, b > 0): $\sqrt{4a}+\sqrt{25a}-6\sqrt{\frac{a}{4}};$ ...

• Bài 9 trang 51 sách bài tập Toán 9 Tập 1: Rút gọn các biểu thức (biết x > 0; y > 0): $2\left(\sqrt{x}+\sqrt{y}\right)-\frac{x-y}{\sqrt{x}+\sqrt{y}};$ ...

• Bài 10 trang 51 sách bài tập Toán 9 Tập 1: Rút gọn và tính giá trị của biểu thức $A=\frac{x-16}{x+\sqrt{x}+1}:\frac{\sqrt{x}+4}{x\sqrt{x}-1}$ tại x = 0,64. ...

• Bài 11 trang 51 sách bài tập Toán 9 Tập 1: Một chiếc thùng hình lập phương có chiều dài cạnh là x (cm) ...