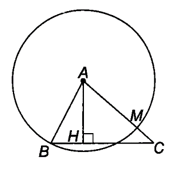
Cho tam giác ABC có AB nhỏ hơn AC và đường cao AH (H.5.12). Trong các điểm B, H và C, điểm nào nằm trong, điểm nào nằm trên
Cho tam giác ABC có AB < AC và đường cao AH (H.5.12).
Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài tập cuối chương 5 - Kết nối tri thức
Bài 5.27 trang 71 sách bài tập Toán 9 Tập 1: Cho tam giác ABC có AB < AC và đường cao AH (H.5.12).
a) Trong các điểm B, H và C, điểm nào nằm trong, điểm nào nằm trên và điểm nào nằm ngoài đường tròn (A; AB)? Vì sao?
b) Xác định vị trí của điểm D trên đoạn AC trong mỗi trường hợp sau:
• Đường tròn (A) và đường tròn (C; CD) tiếp xúc với nhau;
• Đường tròn (A) và đường tròn (C; CD) cắt nhau;
• Đường tròn (A) và đường tròn (C; CD) không giao nhau.
Lời giải:
Dễ thấy điểm B nằm trên (A; AB).
Do AC > AB nên điểm C nằm ngoài (A; AB).
Trong tam giác AHB vuông tại H, AH là cạnh góc vuông, AB là cạnh huyền.
Nên AH < AB, suy ra H nằm trong (A; AB).
b) Do điểm C nằm ngoài (A; AB) nên AC cắt đường tròn tại một điểm nằm giữa A và C. Gọi giao điểm của AC và (A; AB) là M.
Khi đó ta có:
– Hai đường tròn (A) và (C; CD) tiếp xúc với nhau khi D trùng với M;
– Hai đường tròn (A) và (C; CD) cắt nhau khi D nằm giữa A và M;
– Hai đường (A) và (C; CD) không giao nhau khi D nằm giữa C và M.
Lời giải SBT Toán 9 Bài tập cuối chương 5 hay khác: