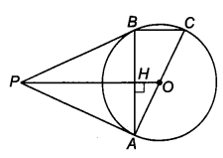
Từ điểm P nằm ngoài đường tròn (O), kẻ hai tiếp tuyến PA và PB đến đường tròn A và B là hai tiếp điểm
Từ điểm P nằm ngoài đường tròn (O), kẻ hai tiếp tuyến PA và PB đến đường tròn (A và B là hai tiếp điểm).
Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài tập cuối chương 5 - Kết nối tri thức
Bài 5.31 trang 71 sách bài tập Toán 9 Tập 1: Từ điểm P nằm ngoài đường tròn (O), kẻ hai tiếp tuyến PA và PB đến đường tròn (A và B là hai tiếp điểm).
a) Chứng minh rằng PO ⊥ AB.
b) Gọi C là điểm đối xứng với A qua O. Chứng minh rằng BC // PO.
c) Tính độ dài các cạnh của tam giác PAB, biết OA = 3 cm và OP = 5 cm.
Lời giải:
a) Vì PA và PB là hai tiếp tuyến của (O) nên PA = PB, suy ra tam giác PAB cân tại P.
Vì PO là đường phân giác của góc APB nên đồng thời cũng là đường trung trực của AB.
Do đó PO ⊥ AB. (đpcm)
b) Vì C đối xứng với A qua O nên OC = OA.
Suy ra C nằm trên đường tròn (O) hay AC là đường kính của (O).
Mà B nằm trên đường tròn (O) nên tam giác ABC vuông tại B, suy ra BC ⊥ AB.
Mà PO ⊥ AB nên BC // PO. (đpcm)
c) PA là tiếp tuyến với (O) tại A nên PA ⊥ OA hay tam giác OAP vuông tại A.
Áp dụng định lý Pythagore cho tam giác OAP nên ta có:
(cm).
Theo câu A ta có PB = PA = 4 cm.
Gọi H là giao điểm của PO với AB.
Vì PO là trung trực của AB và H là giao điểm của PO với AB nên AH ⊥ PO hay tam giác AHP vuông tại H.
Xét tam giác OAP vuông tại A có AH là đường cao, ta có:
(diện tích tam giác AOP)
Hay AH . OP = OA . PA
Suy ra (cm)
AB = 2AH = 2 . 2,4 = 4,8 (cm).
Vậy tam giác PAB có PA = PB = 4 cm và AB = 4,8 cm.
Lời giải SBT Toán 9 Bài tập cuối chương 5 hay khác: