Cho hai đường tròn (O; R) và (O'; R') tiếp xúc ngoài với nhau tại A, hai điểm B thuộc 0 và C thuộc 0

❮ Bài trước Bài sau ❯

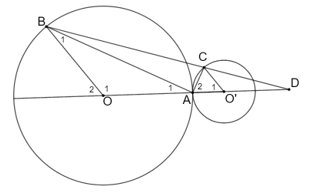
Cho hai đường tròn (O; R) và (O'; R') tiếp xúc ngoài với nhau tại A, hai điểm và sao cho B và C nằm cùng phía đối với đường thẳng OO' và OB // O'C.

Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài tập cuối chương 5 - Kết nối tri thức

Bài 5.34 trang 72 sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O'; R') tiếp xúc ngoài với nhau tại A, hai điểm $B \in (O)$ và $C \in (O)$ sao cho B và C nằm cùng phía đối với đường thẳng OO' và OB // O'C.

a) Chứng minh góc BAC là góc vuông.

b) Cho biết R = 3 cm, R' = 1 cm và BC cắt OO' tại D. Tính độ dài đoạn OD.

Lời giải:

Cho hai đường tròn (O; R) và (O'; R') tiếp xúc ngoài với nhau tại A, hai điểm B thuộc 0 và C thuộc 0

a) Do OA = OB nên tam giác OAB cân tại O, suy ra ${\hat{A}}_{1} = {\hat{B}}_{1}$

Từ đó ta có: ${\hat{A}}_{1} + {\hat{B}}_{1} + {\hat{O}}_{1} = 180 ° = 2 {\hat{A}}_{1} + {\hat{O}}_{1},$ suy ra $2 {\hat{A}}_{1} = 180 ° - {\hat{O}}_{1}$ . (1)

Do O'C = O'A nên tam giác O'AC cân tại O'. Tương tự như trên ta có:

$2 {\hat{A}}_{2} = 180 ° - {\hat{O'}}_{1}$ (2)

Từ (1) và (2), ta có: $2 ({\hat{A}}_{1} + {\hat{A}}_{2}) = 360 ° - ({\hat{O}}_{1} + {\hat{O'}}_{1})$ . (3)

Mà OB // O'C nên ${\hat{O}}_{2} = {\hat{O'}}_{1}$ (hai góc đồng vị).

Do ${\hat{O}}_{2} + {\hat{O}}_{1} = 180 °$ nên ${\hat{O'}}_{1} + {\hat{O}}_{1} = 180 °$ .

Thay vào (3) ta được:

$2 ({\hat{A}}_{1} + {\hat{A}}_{2}) = 360 ° - ({\hat{O}}_{1} + {\hat{O'}}_{1}) = 360 ° - 180 ° = 180 °$ hay ${\hat{A}}_{1} + {\hat{A}}_{2} = \frac{180 °}{2} = 90 °$

Từ đó suy ra $\hat{B A C} = 180 ° - ({\hat{A}}_{1} + {\hat{A}}_{2}) = 180 ° - 90 ° = 90 °$

Do đó góc BAC là góc vuông. (đpcm).

b) Vì O'C // OB nên ∆DOB ᔕ ∆DO'C.

Do đó ta có $\frac{D O}{D O'} = \frac{O B}{O' C} = \frac{3}{1} = 3$

Mà DO' = DO – OO' = DO – (OA + O'A) = DO – (3 + 1) = DO – 4 (cm).

Suy ra $\frac{D O}{D O - 4} = 3$ hay DO = 3(DO – 4). Khi đó DO = 6 cm.

Vậy độ dài đoạn OD là 6 cm.

Lời giải SBT Toán 9 Bài tập cuối chương 5 hay khác:

Xem thêm giải sách bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯

SBT Toán 9 Kết nối tri thức

Cho hai đường tròn (O; R) và (O'; R') tiếp xúc ngoài với nhau tại A, hai điểm B thuộc 0 và C thuộc 0

Xem thêm giải sách bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác: