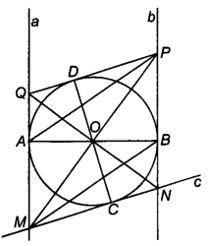
Cho đường tròn (O), đường thẳng a tiếp xúc với (O) tại A, đường thẳng b tiếp xúc với (O) tại B sao cho a // b
Cho đường tròn (O), đường thẳng a tiếp xúc với (O) tại A, đường thẳng b tiếp xúc với (O) tại B sao cho a // b. Gọi C là một điểm tuỳ ý thuộc (O), khác A và B. Tiếp tuyến c của (O) tại C cắt a và b lần lượt tại M và N.
Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài tập cuối chương 5 - Kết nối tri thức
Bài 5.33 trang 72 sách bài tập Toán 9 Tập 1: Cho đường tròn (O), đường thẳng a tiếp xúc với (O) tại A, đường thẳng b tiếp xúc với (O) tại B sao cho a // b. Gọi C là một điểm tuỳ ý thuộc (O), khác A và B. Tiếp tuyến c của (O) tại C cắt a và b lần lượt tại M và N.
a) Chứng minh AB là một đường kính của (O).
b) Gọi D, P và Q lần lượt là các điểm đối xứng với C, M và N qua tâm O. Chứng minh rằng và
c) Chứng minh rằng PQ tiếp xúc với (O) tại D.
d) Chứng minh tứ giác MNPQ là một hình thoi.
Lời giải:
a) MA, MN và BN là các tiếp tuyến của (O) nên
+ Xét tứ giác ABMN có
Suy ra . (1)
+ Xét tứ giác AOCM có .
Suy ra . (2)
+ Xét tứ giác OBNC có .
Suy ra . (3)
Từ (1), (2) và (3), suy ra hay A, O, B thẳng hàng.
Mà A và O nằm trên (O) nên AB là đường kính của (O). (đpcm)
b) Vì và D đối xứng với C qua O nên . (đpcm)
Xét tứ giác AMBP có:
OA = OB (bán kính của (O))
OM = OP (P đối xứng với M qua O)
Suy ra hai đường chéo của tứ giác AMBP cắt nhau tại trung điểm mỗi đường.
Do đó AMBP là hình bình hành, vì vậy BP // AM hay BP // a.
Mà b // a nên BP trùng với b hay . (đpcm)
Xét tứ giác AQBN có:
OA = OB (bán kính của (O))
ON = OQ (Q đối xứng với N qua O)
Suy ra hai đường chéo của tứ giác AQBN cắt nhau tại trung điểm mỗi đường.
Do đó AQBN là hình bình hành, vì vậy AQ // BN hay AQ // b.
Mà b // a nên AQ trùng với a hay . (đpcm)
c) Xét ∆COM và ∆DOP có:
OM = OP (M và PO đối xứng qua O)
OC = OD (C và D đối xứng qua O)
(hai góc đối đỉnh)
Do đó ∆COM = ∆DOP (c.g.c), suy ra
Tương tự, ta có ∆CON = ∆DOQ (c.g.c), suy ra
Do đó hay P, D, Q thẳng hàng.
Mà nên PQ là tiếp tuyến của (O) tại D.
d) Tứ giác MNPQ có hai đường chéo MP và NQ cắt nhau tại trung điểm O của mỗi đường (do M và P, N và Q đối xứng với nhau qua O) nên MNPQ là hình bình hành.
Hai tiếp tuyến AM và CM của (O) cắt nhau tại M nên
Hai tiếp tuyến BN và CN của (O) cắt nhau tại N nên
Từ đó ta có:
Suy ra MP ⊥ NQ. Mà MNPQ là hình bình hành nên hai đường chéo của hình bình hành MNPQ vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.
Do đó MNPQ là hình thoi. (đpcm)
Lời giải SBT Toán 9 Bài tập cuối chương 5 hay khác: