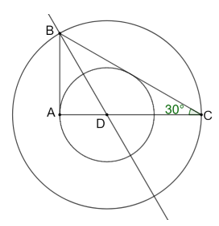
Cho tam giác vuông ABC góc A = 90 độ có góc C = 30 độ và AB = 3 cm. Đường phân giác của góc B cắt AC tại D

Cho tam giác vuông ABC có và AB = 3 cm. Đường phân giác của góc B cắt AC tại D.

Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài tập cuối chương 5 - Kết nối tri thức

Bài 5.30 trang 71 sách bài tập Toán 9 Tập 1: Cho tam giác vuông ABC $(\hat{A} = 90 °)$ có $\hat{C} = 30 °$ và AB = 3 cm. Đường phân giác của góc B cắt AC tại D.

a) Chứng minh rằng đường tròn (D; DA) tiếp xúc với cạnh BC.

b) Tính độ dài cung nằm trong góc BDC của đường tròn (D; DA) và diện tích hình quạt tròn tương ứng với cung ấy.

c) Tính diện tích hình vành khuyên tạo bởi hai đường tròn (D; DA) và (D; DC).

Lời giải:

Cho tam giác vuông ABC góc A = 90 độ có góc C = 30 độ và AB = 3 cm. Đường phân giác của góc B cắt AC tại D

a) Kẻ đường vuông góc từ D xuống BC cắt BC tại E.

Do BD là đường phân giác của hóc ABC nên DA = DE.

Vậy E nằm trên đường tròn (D; DA) hay (D; DA) tiếp xúc với cạnh BC. (đpcm)

b) Tam giác ABC vuông tại A nên ta có:

$\hat{A B C} = 90 ° - \hat{A C B} = 90 ° - 30 ° = 60 °$

DB là phân giác của góc ABC nên ta có:

$\hat{A B D} = \hat{D B C} = \frac{\hat{A B C}}{2} = \frac{60 °}{2} = 30 °$

Xét tam giác BDC ta có:

$\hat{B D C} = 180 ° - \hat{D B C} - \hat{D C B} = 180 ° - 30 ° - 30 ° = 120 °$

Xét ta giác ABD vuông tại A ta có:

$A D = A B \tan 30 ° = 3. \tan 30 ° = \sqrt{3}$ (cm)

Độ dài cung nằm trong góc BDC của đường tròn (D; DA) là:

$\frac{n}{180} π R = \frac{120}{180} π \cdot \sqrt{3} = \frac{2 \sqrt{3}}{3} π$ (cm)

Diện tích hình quạt tròn tương ứng với cung đó là:

$\frac{n}{360} π R^{2} = \frac{120}{360} π \cdot {(\sqrt{3})}^{2} = π$ (cm²)

Độ dài cung nằm trong góc BDC của đường tròn (D; DA) là:

$\frac{n}{180} π R = \frac{120}{180} π \cdot \sqrt{3} = \frac{2 \sqrt{3}}{3} π$ (cm)

Vậy độ dài cung nằm trong góc BDC của đường tròn (D; DA) là $\frac{2 \sqrt{3}}{3} π$ cm và diện tích hình quạt tròn tương ứng với cung đó là π cm².

c) Do $\hat{D B C} = \hat{D C B} = 30 °$ nên tam giác DBC cân tại D, suy ra DC = DB.

Xét tam giác vuông ABD, ta có:

$B D = \frac{A B}{\cos \hat{A B D}} = \frac{2}{\cos 30 °} = 2 \sqrt{3}$ (cm), suy ra $D C = D B = 2 \sqrt{3}$ cm).

Ta có đường tròn (D; DA) có bán kính DA = $\sqrt{3}$ cm, đường tròn (D; DC) có bán kính $D C = 2 \sqrt{3}$ cm.

Do đó diện tích hình vành khuyên tạo bởi hai đường tròn này là:

$[{(2 \sqrt{3})}^{2} - {(\sqrt{3})}^{2}] π = 9 π$ (cm²).

Vậy diện tích hình vành khuyên tạo bởi hai đường tròn (D; DA) và (D; DC) là 9π cm².

Lời giải SBT Toán 9 Bài tập cuối chương 5 hay khác:

SBT Toán 9 Kết nối tri thức

Cho tam giác vuông ABC góc A = 90 độ có góc C = 30 độ và AB = 3 cm. Đường phân giác của góc B cắt AC tại D

Xem thêm giải sách bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác: