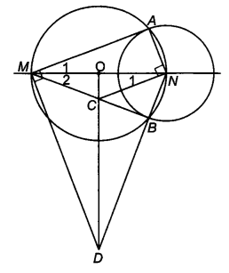
Cho đường tròn tâm O, đường kính MN. Một đường tròn (N) cắt (O) tại A và B

Cho đường tròn tâm O, đường kính MN. Một đường tròn (N) cắt (O) tại A và B.

Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài tập cuối chương 5 - Kết nối tri thức

Bài 5.35 trang 72 sách bài tập Toán 9 Tập 1: Cho đường tròn tâm O, đường kính MN. Một đường tròn (N) cắt (O) tại A và B.

a) Chứng minh rằng MA và MB là hai tiếp tuyến của (N).

b) Đường thẳng qua N và vuông góc với NA cắt MB tại C. Chứng minh hai điểm M và N đối xứng với nhau qua OC.

c) Đường thẳng qua M và vuông góc với MA cắt NB tại D. Chứng minh ba điểm O, C và D thẳng hàng.

Lời giải:

Cho đường tròn tâm O, đường kính MN. Một đường tròn (N) cắt (O) tại A và B

a) Vì MN là đường kính của (O), A là một điểm nằm trên (O) nên tam giác MAN vuông tại A hay MA ⊥ AN.

Mà A nằm trên (N) nên MA là tiếp tuyến tại A của (N). (đpcm)

Mặt khác, MN là đường kính của (O), B là một điểm nằm trên (O) nên tam giác MBN vuông tại A hay MB ⊥ BN.

Mà B nằm trên (N) nên MB là tiếp tuyến tại B của (N). (đpcm)

b) Vì AM ⊥ AN và CN ⊥ AN nên AM // CM, suy ra ${\hat{M}}_{1} = {\hat{N}}_{1}$ (hai góc so le trong).

Mà MA và MN là hai tiếp tuyến của (N) nên MN là đường phân giác của góc AMB hay ${\hat{M}}_{1} = {\hat{M}}_{2}$

Do đó ${\hat{M}}_{2} = {\hat{M}}_{1} = {\hat{N}}_{1}$ , suy ra tam giác CMN cân tại C.

Tam giác CMN cân tại C có OM = ON nên OC là trung tuyến của CO và đồng thời là trung trực của MN.

Vậy M và N đối xứng với nhau qua OC. (đpcm)

c) Do MD ⊥ MA và AN ⊥ AM nên MD // AN, do đó $\hat{D N M} = \hat{A N M}$ .

Mà MA và MN là hai tiếp tuyến cắt nhau của (N) nên MN là đường phân giác của góc ANB. Do đó $\hat{D N M} = \hat{A N M}$

Tử đó suy ra $\hat{D M N} = \hat{D N M} = \hat{A N M}$ , do đó tam giác DMN cân tại D.

Tam giác DMN cân tại D nên D nằm trên đường trung trực CO của MN hay ba điểm O, C, D thẳng hàng. (đpcm).

Lời giải SBT Toán 9 Bài tập cuối chương 5 hay khác:

SBT Toán 9 Kết nối tri thức