Cho hình thang cân ABCD (AB // CD). Chứng minh rằng đường trung trực d của AB cũng là đường trung trực của CD
Cho hình thang cân ABCD (AB // CD).
Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài tập cuối chương 5 - Kết nối tri thức
Bài 5.28 trang 71 sách bài tập Toán 9 Tập 1: Cho hình thang cân ABCD (AB // CD).
a) Chứng minh rằng đường trung trực d của AB cũng là đường trung trực của CD (từ đó suy ra hai điểm A và B đối xứng với nhau, C và D đối xứng với nhau qua d).
b) Giải thích tại sao nếu một đường tròn đi qua 3 điểm A, B và C thì nó cũng đi qua điểm D.
Lời giải:
a) TH1: DA // CB
Do ABCD là hình thang cân mà DA // CB nên ABCD là hình chữ nhật.
Do đó đường trung trực d của AB cũng là đường trung trực của CD. (đpcm)
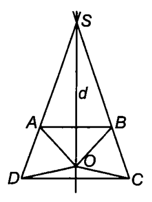
TH2: DA và CB cắt nhau tại S.
Mà ABCD là hình thang cân nên
Suy ra SAB và SDC cân tại S (hai góc ở đáy bằng nhau).
Do đó trong tam giác SAB cân tại S, đường trung trực d của AB cũng là đường phân giác của góc S.
Trong tam giác SCD cân tại S, đường phân giác d của góc S cũng là đường trung trực của CD.
Vậy đường trung trực d của AB cũng là đường trung trực của CD. (đpcm)
b) Giả sử O là tâm đường tròn đi qua 3 điểm A, B, C.
Khi đó OA = OB, suy ra đường trung trực d của AB đi qua O.
Mà đường trung trực của AB cũng là đường trung trực của CD nên O cũng nằm trên đường trung trực của CD.
Từ đó suy ra OC = OD.
Vậy D cũng thuộc đường tròn (O). (đpcm)
Lời giải SBT Toán 9 Bài tập cuối chương 5 hay khác: