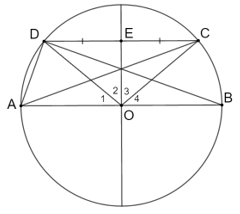
Giả sử CD là một dây song song với đường kính AB của đường tròn (O) sao cho ABCD là một tứ giác lồi

❮ Bài trước Bài sau ❯

Giả sử CD là một dây song song với đường kính AB của đường tròn (O) sao cho ABCD là một tứ giác lồi. Gọi E là trung điểm của đoạn CD.

Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài tập cuối chương 5 - Kết nối tri thức

Bài 5.29 trang 71 sách bài tập Toán 9 Tập 1: Giả sử CD là một dây song song với đường kính AB của đường tròn (O) sao cho ABCD là một tứ giác lồi. Gọi E là trung điểm của đoạn CD.

a) Chứng minh rằng A đối xứng với B và C đối xứng với D qua đường thẳng OE.

b) Chứng minh rằng tứ giác ABCD là một hình thang cân.

c) Biết rằng AB = 12 cm và $\hat{C O D} = 100 °$ . Tính độ dài cung (nhỏ) AD và cung (lớn) ABC.

d) Với giả thiết ở câu c, tính diện tích hình quạt tròn ứng với cung nhỏ BD.

Lời giải:

Giả sử CD là một dây song song với đường kính AB của đường tròn (O) sao cho ABCD là một tứ giác lồi

a) Vì E là trung điểm của CD nên EC = ED.

Vì C và D nằm trên (O) nên OC = OD.

Do đó OE là đường trung trực của CD hay C và D đối xứng với nhau qua OE. (đpcm)

Từ đó suy ra OE ⊥ CD.

Mà CD // AB nên OE ⊥ AB.

Mặt khác OA = OB nên OE cũng là đường trung trực của AB, hay A và B đối xứng với nhau qua OE. (đpcm)

b) Vì OC = OD nên tam giác OCD cân tại O và OE là đường trung trực nên cũng là đường phân giác của góc COD hay ${\hat{O}}_{2} = {\hat{O}}_{3}$ .

Suy ra: $\hat{A O C} = \hat{A O E} + \hat{E O C} = 90 ° + {\hat{O}}_{3} = {\hat{O}}_{2} + 90 °$ $= \hat{D O E} + \hat{E O B} = \hat{D O B}$

Hai tam giác AOC và DOB cân tại O có:

Các cạnh bên bằng nhau (OA = OB = OC = OD và bằng bán kính đường tròn (O))

Góc ở đỉnh bằng nhau ( $\hat{A O C} = \hat{D O B}$ ).

Suy ra ∆AOC = ∆DOB, vì vậy AC = DB.

Vậy hình thang ABCD (AB // CD) có hai đường chéo bằng nhau nên ABCD là hình thang cân.

c) Do đường kính AB = 12 cm độ dài bán kính đường tròn (O) là:

12 : 2 = 6 (cm)

Ta có: ${\hat{O}}_{2} = {\hat{O}}_{3} = \frac{\hat{C O D}}{2} = \frac{100 °}{2} = 50 °$

$\hat{A O C} = \hat{A O E} + {\hat{O}}_{2} = 90 ° + 50 ° = 140 °$

Số đo cung nhỏ AD là:

$s đ \overset{⏜}{A D} = \hat{A O D} = 90 ° - {\hat{O}}_{2} = 90 ° - 50 ° = 40 °$

Độ dài cung nhỏ AD là:

$\frac{n}{180} π R = \frac{40}{180} . π .6 = \frac{4}{3} π$ (cm)

Số đo cung lớn ABC là:

sđ $\overset{⏜}{A B C} = 360 ° - \hat{A O C} = 360 ° - 140 ° = 220 °$

Độ dài cung lớn ABC là:

$\frac{n}{180} π R = \frac{220}{180} π \cdot 6 = \frac{22}{3} π$ (cm)

Vậy độ dài cung nhỏ AD là $\frac{4}{3} π$ cm và độ dài cung lớn ABC là $\frac{22}{3} π$ cm.

d) Ta có $\hat{B O D} = \hat{B O E} + \hat{O_{2}} = 90 ° + 50 ° = 140 °$

Diện tích hình quạt tròn ứng với cung nhỏ BD là:

$\frac{n}{360} π R^{2} = \frac{140}{360} π \cdot 6^{2} = 14 π$ (cm²)

Vậy diện tích hình quạt tròn ứng với cung nhỏ BD là 14π cm².

Lời giải SBT Toán 9 Bài tập cuối chương 5 hay khác:

Xem thêm giải sách bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯

SBT Toán 9 Kết nối tri thức

Giả sử CD là một dây song song với đường kính AB của đường tròn (O) sao cho ABCD là một tứ giác lồi

Xem thêm giải sách bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác: