Giải Toán 10 trang 90 Tập 1 Cánh diều

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 90 Tập 1 trong Bài 5: Tích của một số với một vectơ Toán lớp 10 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 90.

Giải Toán 10 trang 90 Tập 1 Cánh diều

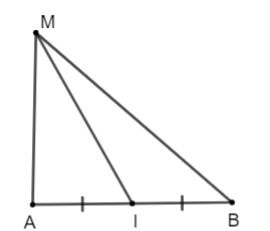
Hoạt động 3 trang 90 Toán lớp 10 Tập 1: Cho I là trung điểm của đoạn thẳng AB và điểm M tùy ý. Chứng minh rằng $\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}$ .

Lời giải:

Do I là trung điểm của AB nên $\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}$.

Khi đó: 

$$\begin{gathered} \overrightarrow{MA}+\overrightarrow{MB}=\left(\overrightarrow{MI}+\overrightarrow{IA}\right)+\left(\overrightarrow{MI}+\overrightarrow{IB}\right) \\ =2\overrightarrow{MI}+\left(\overrightarrow{IA}+\overrightarrow{IB}\right) \end{gathered}$$

$=2\overrightarrow{MI}+\overrightarrow{0}=2\overrightarrow{MI}$

Vậy $\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}$.

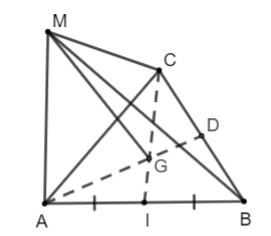
Hoạt động 4 trang 90 Toán lớp 10 Tập 1: Cho G là trọng tâm của tam giác ABC và điểm M tùy ý. Chứng minh rằng $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$ .

Lời giải:

Do G là trọng tâm của tam giác ABC nên $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$.

Ta có:

$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}$

$=\left(\overrightarrow{MG}+\overrightarrow{GA}\right)+\left(\overrightarrow{MG}+\overrightarrow{GB}\right)+\left(\overrightarrow{MG}+\overline{GC}\right)$

$=3\overrightarrow{MG}+\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)$

$=3\overrightarrow{MG}+\overrightarrow{0}=3\overrightarrow{MG}$

Vậy $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$.

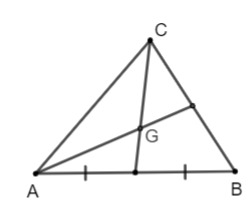
Luyện tập 3 trang 90 Toán lớp 10 Tập 1: Cho tam giác ABC có G là trọng tâm. Chứng minh $\overrightarrow{AB}+\overrightarrow{AC}=3\overrightarrow{AG}$ .

Lời giải:

Do G là trọng tâm của tam giác ABC nên $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$.

Ta có:

$\overrightarrow{AB}+\overrightarrow{AC}=\left(\overrightarrow{AG}+\overrightarrow{GB}\right)+\left(\overrightarrow{AG}+\overrightarrow{GC}\right)$

$=2\overrightarrow{AG}+\overrightarrow{GB}+\overrightarrow{GC}$

$=2\overrightarrow{AG}+\overrightarrow{GB}+\overrightarrow{GC}+\left(\overrightarrow{AG}-\overrightarrow{AG}\right)$

$=3\overrightarrow{AG}+\overrightarrow{GB}+\overrightarrow{GC}+\left(-\overrightarrow{AG}\right)$

$=3\overrightarrow{AG}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GA}$

$=3\overrightarrow{AG}+\overrightarrow{0}=3\overrightarrow{AG}$.

Vậy $\overrightarrow{AB}+\overrightarrow{AC}=3\overrightarrow{AG}$.

Lời giải bài tập Toán lớp 10 Bài 5: Tích của một số với một vectơ Cánh diều hay khác:

• Giải Toán 10 trang 88 Tập 1
• Giải Toán 10 trang 89 Tập 1
• Giải Toán 10 trang 91 Tập 1
• Giải Toán 10 trang 92 Tập 1