Gọi G là trọng tâm tam giác đều ABC có cạnh bằng a. Mệnh đề nào sau đây là sai?

❮ Bài trước Bài sau ❯

Câu hỏi:

A. $\vec{A B} . \vec{A C} = \frac{1}{2} a^{2};$

B. $\vec{A C} . \vec{C B} = - \frac{1}{2} a^{2};$

C. $\vec{G A} . \vec{G B} = \frac{a^{2}}{6};$

D. $\vec{A B} . \vec{A G} = \frac{1}{2} a^{2} .$

Trả lời:

Đáp án đúng là: C

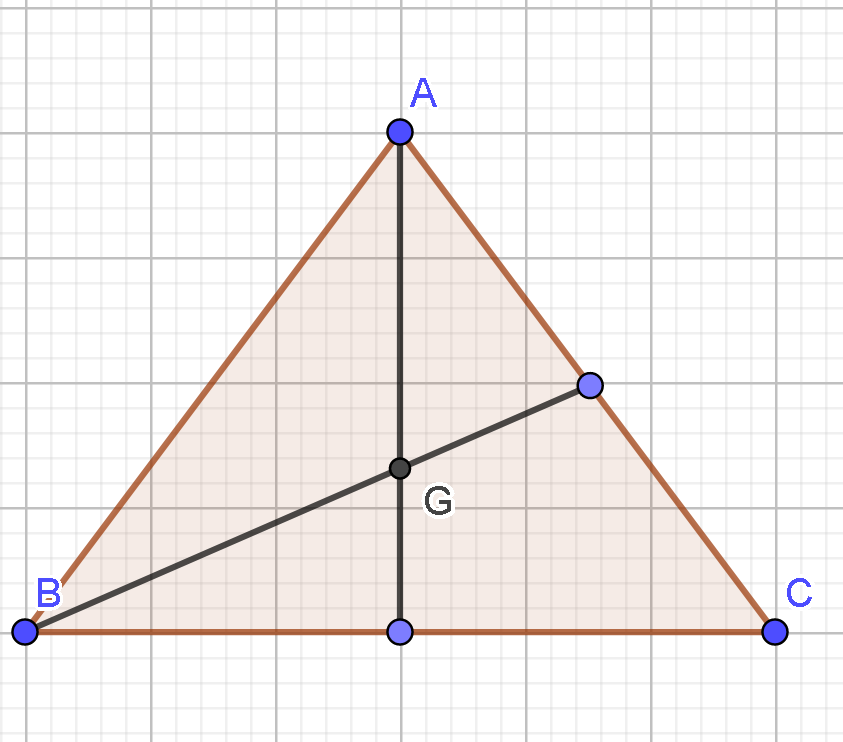
- Xác định được góc $(\vec{A B}, \vec{A C})$ là góc $\hat{A}$ nên $(\vec{A B}, \vec{A C}) = 60^{0}$ (do tam giác ABC đều)

Do đó $\vec{A B} . \vec{A C} = A B . A C . c o s (\vec{A B}, \vec{A C}) = a . a . c o s 60^{0} = \frac{a^{2}}{2}$ $\Rightarrow$ A đúng

- Xác định được góc $(\vec{A C}, \vec{C B})$ là góc ngoài của góc $\hat{C}$ nên $(\vec{A C}, \vec{C B}) = 120^{0} .$

Do đó $\vec{A C} . \vec{C B} = A C . C B . c o s (\vec{A C}, \vec{C B}) = a . a . c o s 120^{0} = - \frac{a^{2}}{2} \Rightarrow$ B đúng.

Xác định được góc $(\vec{G A}, \vec{G B})$ là góc $\hat{A G B}$ nên $(\vec{G A}, \vec{G B}) = 120^{0} .$

Ta có: AG nằm trên đường trung tuyến cũng chính là đường cao của tam giác đều ABC, ta tính được đường cao, suy ra: AG = $\frac{2}{3}$ .a. $\frac{\sqrt{3}}{2}$ = $\frac{a}{\sqrt{3}}$ .

Tương tự, GB = $\frac{a}{\sqrt{3}}$ .

Do đó $\vec{G A} . \vec{G B} = G A . G B . c o s (\vec{G A}, \vec{G B}) = \frac{a}{\sqrt{3}} . \frac{a}{\sqrt{3}} . c o s 120^{0} = - \frac{a^{2}}{6} \Rightarrow$ C sai.

Xác định được góc $(\vec{A B}, \vec{A G})$ là góc $\hat{G A B}$ nên $(\vec{A B}, \vec{A G}) = 30^{0} .$

Do đó $\vec{A B} . \vec{A G} = A B . A G . c o s (\vec{A B}, \vec{A G}) = a . \frac{a}{\sqrt{3}} . c o s 30^{0} = \frac{a^{2}}{2} \Rightarrow$ D đúng.

Xem thêm bài tập Toán 10 Cánh diều có lời giải hay khác:

Câu 1:

Cho $\vec{a}$ và $\vec{b}$ là hai vectơ cùng hướng và đều khác vectơ $\vec{0}$ . Mệnh đề nào sau đây đúng?

Xem lời giải »

Câu 2:

Cho $\vec{a}$ và $\vec{b}$ khác vectơ $\vec{0}$ . Xác định góc $α$ giữa hai vectơ $\vec{a}$ và $\vec{b}$ khi $\vec{a} . \vec{b} = - |\vec{a}| . |\vec{b}| .$

Xem lời giải »

Câu 3:

Cho hai vectơ $\vec{a}$ và $\vec{b}$ thỏa mãn $|\vec{a}| = 3,$ $|\vec{b}| = 2$ và $\vec{a} . \vec{b} = - 3.$ Xác định góc $α$ giữa hai vectơ $\vec{a}$ và $\vec{b}$

Xem lời giải »

Câu 4:

Cho hai vectơ $\vec{a}$ và $\vec{b}$ thỏa mãn $|\vec{a}| = |\vec{b}| = 1$ và hai vectơ $\vec{u} = \frac{2}{5} \vec{a} - 3 \vec{b}$ và $\vec{v} = \vec{a} + \vec{b}$ vuông góc với nhau. Xác định góc $α$ giữa hai vectơ $\vec{a}$ và $\vec{b}$ .