Bài 1 trang 17 Toán 10 Tập 2 Chân trời sáng tạo

Giải phương trình sau:

Giải Toán lớp 10 Bài 3: Phương trình quy về phương trình bậc hai

Bài 1 trang 17 Toán lớp 10 Tập 2: Giải phương trình sau:

a) $\sqrt{11 x^{2} - 14 x - 12} = \sqrt{3 x^{2} + 4 x - 7};$

b) $\sqrt{x^{2} + x - 42} = \sqrt{2 x - 30};$

c) $2 \sqrt{x^{2} - x - 1} = \sqrt{x^{2} + 2 x + 5};$

d) $3 \sqrt{x^{2} + x - 1} - \sqrt{7 x^{2} + 2 x - 5} = 0.$

Lời giải:

a) $\sqrt{11 x^{2} - 14 x - 12} = \sqrt{3 x^{2} + 4 x - 7};$

⇒ 11x² – 14x – 12 = 3x² + 4x – 7

⇒ 8x² – 18x – 5 = 0

⇒ x = $\frac{5}{2}$ hoặc x = $- \frac{1}{4}$

Thay lần lượt các giá trị của x vào phương trình đã cho ta thấy chỉ có x = $\frac{5}{2}$ là thỏa mãn.

Vậy tập nghiệm của phương trình S = 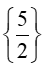Bài 1 trang 17 Toán lớp 10 Tập 2 Chân trời sáng tạo | Giải Toán lớp 10 .

b) $\sqrt{x^{2} + x - 42} = \sqrt{2 x - 30}$

⇒ x² + x – 42 = 2x – 30

⇒ x² – x – 12 = 0

⇒ x = - 3 hoặc x = 4

Thay lần lượt x = -3 và x = 4 vào phương trình đã cho ta thấy không có giá trị nào thỏa mãn.

Vậy tập nghiệm của phương trình S = $\emptyset$ .

c) $2 \sqrt{x^{2} - x - 1} = \sqrt{x^{2} + 2 x + 5};$

⇒ 4x² – 4x – 4 = x² + 2x + 5

⇒ 3x² – 6x – 9 = 0

⇒ x = -1 hoặc x = 3

Thay lần lượt các giá trị này vào phương trình đã cho ta thấy x = -1 hoặc x = 3 đều thỏa mãn.

Vậy nghiệm của phương trình là x = -1 và x = 3.

d) $3 \sqrt{x^{2} + x - 1} - \sqrt{7 x^{2} + 2 x - 5} = 0$

⇔ $3 \sqrt{x^{2} + x - 1} = \sqrt{7 x^{2} + 2 x - 5}$

⇒ 9(x² + x – 1) = 7x² + 2x – 5

⇒ 9x² + 9x – 9 = 7x² + 2x – 5

⇒ 2x² + 7x – 4 = 0

⇒ x = -4 và x = $\frac{1}{2}$

Thay lần lượt hai giá trị này vào phương trình đã cho ta thấy chỉ có x = -4 thỏa mãn.

Vậy nghiệm của phương trình là x = -4.

Lời giải bài tập Toán 10 Bài 3: Phương trình quy về phương trình bậc hai hay, chi tiết khác: