Cho góc alpha (0 độ bé hơn bằng alpha bé hơn bằng 180 độ). Trong các khẳng định

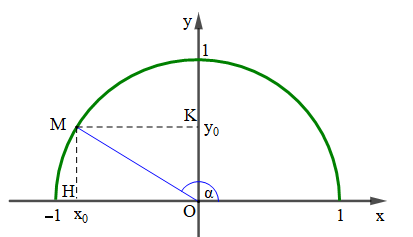
Khi đó ta có: OH = x₀ = cosα, MH = OK = y₀ = sinα, OM = 1.

Tam giác OMH vuông tại H, áp dụng định lí Pythagore ta có:

MH² + OH² = OM²

Hay sin²α + cos²α = 1.

Do đó phương án A là mệnh đề đúng.

Với 0° < α < 180° và α ≠ 90° ta có: $\tan \alpha =\frac{y_0}{x_0};$$\cot \alpha =\frac{x_0}{y_0}.$

$\Rightarrow \tan \alpha .\cot \alpha =\frac{y_0}{x_0}.\frac{x_0}{y_0}=1.$ Do đó phương án B là mệnh đề đúng.

Với α ≠ 90° ta có: $1+{\tan }^2\alpha =1+\frac{{\sin }^2\alpha }{{\text{cos}}^2\alpha }=\frac{{\text{cos}}^2\alpha +{\sin }^2\alpha }{{\text{cos}}^2\alpha }=\frac{1}{co{s}^2\alpha }$ (do sin²α + cos²α = 1).

Do đó phương án C là mệnh đề đúng.

Với 0° < α < 180° và α ≠ 90° ta có:

$1+{\cot }^2\alpha =1+\frac{{\cot }^2\alpha }{{\sin }^2\alpha }=\frac{{\sin }^2\alpha +{\cos }^2\alpha }{{\sin }^2\alpha }=\frac{1}{{\sin }^2\alpha }$(do sin²α + cos²α = 1).

Do đó phương án D là mệnh đề sai.

Vậy ta chọn phương án D.