Cho hình chữ nhật ABCD có AB = căn bậc hai 2 , AD = 1. Tính góc giữa hai vectơ AC 

Câu hỏi:

Trả lời:

Hướng dẫn giải

Đáp án đúng là: C

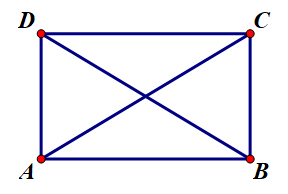
Tam giác ACD vuông tại D: $\cos \widehat{CAD}=\frac{AD}{AC}$.

Tam giác ABC vuông tại B: $\cos \widehat{CAD}=\frac{AD}{AC}$.

Ta có $\overrightarrow{AC}.\overrightarrow{BD}=\overrightarrow{AC}.\left(\overrightarrow{AD}-\overrightarrow{AB}\right)=\overrightarrow{AC}.\overrightarrow{AD}-\overrightarrow{AC}.\overrightarrow{AB}$.

$=AC.AD.\cos \widehat{CAD}-AC.AB.\cos \widehat{CAB}$

$=AC.AD.\frac{AD}{AC}-AC.AB.\frac{AB}{AC}$

$=A{D}^2-A{B}^2=1-2=-1$.

Vì ABCD là hình chữ nhật nên ta có CD = AB = $\sqrt{2}$ và AC = BD.

Tam giác ACD vuông tại D: $A{C}^2=A{D}^2+C{D}^2$ (Định lý Pytago)

$\iff A{C}^2=1^2+{\left(\sqrt{2}\right)}^2=3$

$\Rightarrow AC=\sqrt{3}$.

Do đó BD = AC = $\sqrt{3}$.

Lại có: $\overrightarrow{AC}.\overrightarrow{BD}=AC.BD.\cos \left(\overrightarrow{AC},\overrightarrow{BD}\right)$

$\iff -1=\sqrt{3}.\sqrt{3}.\cos \left(\overrightarrow{AC},\overrightarrow{BD}\right)$

$\iff \cos \left(\overrightarrow{AC},\overrightarrow{BD}\right)=\frac{-1}{3}$.

$\Rightarrow \left(\overrightarrow{AC},\overrightarrow{BD}\right)\approx 109°{28}^{\text{'}}$.

Vậy ta chọn đáp án C.