Cho tam giác đều ABC có đường cao AH. Tính vecto AH, BA
Câu hỏi:
Cho tam giác đều ABC có đường cao AH. Tính .
A. 30°;
B. 60°;
C. 120°;
D. 150°.
Trả lời:
Hướng dẫn giải
Đáp án đúng là: D
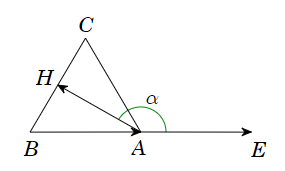
Vẽ .
Khi đó ta có .
Tam giác ABC đều có AH là đường cao.
Suy ra AH cũng là đường phân giác của tam giác ABC.
Tam giác ABC đều, suy ra .
Do đó .
Ta có: (hai góc kề bù)
.
Vậy ta chọn đáp án D.

