Hàm số y = f(x) có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng? A. Hàm số nghịch biến trên khoảng (0; 3); B. Hàm số đồng biến trên khoảng (–∞; 1); C.
Câu hỏi:
Hàm số y = f(x) có đồ thị như hình vẽ bên.
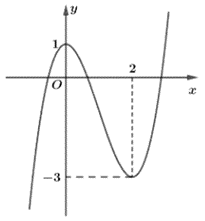
Khẳng định nào sau đây đúng?
Trả lời:
Hướng dẫn giải
Đáp án đúng là: C
Từ đồ thị, ta thấy hàm số xác định trên ℝ.
+) Trên khoảng (–∞; 0), đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (–∞; 0).
+) Trên khoảng (0; 2), đồ thị có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (0; 2).
+) Trên khoảng (2; +∞), đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (2; +∞).
Phương án A sai vì hàm số đồng biến trên (–∞; 0) và (2; 3); nhưng nghịch biến trên khoảng (0; 2).
Phương án B sai vì hàm số đồng biến trên (–∞; 0) nhưng nghịch biến trên khoảng (0; 1).
Phương án C đúng.
Phương án D sai vì hàm số đồng biến trên (–3; 0) và (2; +∞) nhưng nghịch biến trên khoảng (0; 2).
Vậy ta chọn phương án C.

