Giải Toán 10 trang 67 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 67 Tập 2 trong Bài 4: Ba đường conic trong mặt phẳng toạ độ Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 67.

Giải Toán 10 trang 67 Tập 2 Chân trời sáng tạo

Thực hành 2 trang 67 Toán lớp 10 Tập 2: Viết phương trình chính tắc của hypebol có tiêu cự bằng 10 và độ dài trục ảo bằng 6.

Lời giải:

Tiêu cự của hypebol là: 2c = 10 ⇔ c = 5 và độ dài trục ảo là 2b = 6 ⇔ b = 3.

Ta có: $\sqrt{a^2+b^2}=c$

⇔ a² + b² = c²

⇔ a² = c² – b² = 5² – 3² = 25 – 9 = 16

⇔ a = 4

Khi đó phương trình chính tắc của hypebol có tiêu cự bằng 10 và độ dài trục ảo bằng 6 là:

$\frac{x^2}{4^2}-\frac{y^2}{3^2}=1$

⇔ $\frac{x^2}{16}-\frac{y^2}{9}=1$.

Vậy phương trình chính tắc của hypebol cần tìm là: $\frac{x^2}{16}-\frac{y^2}{9}=1$.

Vận dụng 2 trang 67 Toán lớp 10 Tập 2: Một tháp làm nguội của một nhà máy có mặt cắt là một hypebol có phương trình $\frac{x^2}{{27}^2}-\frac{y^2}{{40}^2}=1$ (Hình 9). Cho biết chiều cao của tháp là 120m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng một nửa khoảng cách từ tâm đối xứng đến đáy. Tính bán kính đường tròn nóc và bán kính đường tròn đáy của tháp.

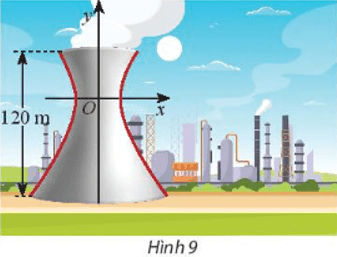
Lời giải:

Gọi khoảng cách từ nóc tháp đến tâm đối xứng của hypebol là h thì khoảng cách từ tâm đối xứng đến đáy là 2h.

Khi đó chiều cao của tháp là: h + 2h = 3h

Mà chiều cao của tháp là 120m nên ta có: 3h = 120 ⇔ h = 120 : 3 = 40 (m).

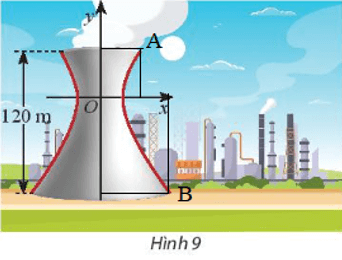
Gọi A và B là hai điểm như hình vẽ.

Ta có khoảng cách từ nóc tháp đến tâm đối xứng của hypebol cũng chính là khoảng cách từ điểm A đến trục hoành hay là tung độ của điểm A.

⇒ y_A = 40.

Vì A thuộc hypebol nên tọa độ điểm A thỏa mãn phương trình $\frac{x^2}{{27}^2}-\frac{y^2}{{40}^2}=1$

⇒ $\frac{x_A^2}{{27}^2}-\frac{y_A^2}{{40}^2}=1$

⇔ $\frac{x_A^2}{{27}^2}-\frac{{40}^2}{{40}^2}=1$

⇔ $\frac{x_A^2}{{27}^2}-1=1$

⇔ $\frac{x_A^2}{{27}^2}=2$

⇔ $x_A^2={2.27}^2$

⇔ $x_A=27\sqrt{2}$

⇒ $A\left(27\sqrt{2};40\right)$

Mặt khác điểm A thuộc đường tròn nóc nên khoảng cách từ A đến tâm đường tròn là bán kính của đường tròn và bằng 27$\sqrt{2}$.

Ta có khoảng cách từ nóc tháp đến tâm đối xứng của hypebol cũng chính là khoảng cách từ điểm B đến trục hoành hay là tung độ của điểm B.

⇒ y_B = 2h = 2.40 = 80.

Vì B thuộc hypebol nên tọa độ điểm B thỏa mãn phương trình $\frac{x^2}{{27}^2}-\frac{y^2}{{40}^2}=1$

⇒ $\frac{x_B^2}{{27}^2}-\frac{y_B^2}{{40}^2}=1$

⇔ $\frac{x_B^2}{{27}^2}-\frac{{80}^2}{{40}^2}=1$

⇔ $\frac{x_B^2}{{27}^2}-4=1$

⇔ $\frac{x_B^2}{{27}^2}=5$

⇔ $x_B^2={5.27}^2$

⇔ $x_B=27\sqrt{5}$

⇒ $B\left(27\sqrt{5};80\right)$

Mặt khác điểm B thuộc đường tròn nóc nên khoảng cách từ B đến tâm đường tròn là bán kính của đường tròn và bằng 27$\sqrt{5}$.

Vậy bán kính đường tròn nóc là 27$\sqrt{2}$ và bán kính đường tròn đáy là 27$\sqrt{5}$.

Lời giải bài tập Toán lớp 10 Bài 4: Ba đường conic trong mặt phẳng toạ độ Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 63 Tập 2

• Giải Toán 10 trang 64 Tập 2

• Giải Toán 10 trang 65 Tập 2

• Giải Toán 10 trang 66 Tập 2

• Giải Toán 10 trang 68 Tập 2

• Giải Toán 10 trang 70 Tập 2

• Giải Toán 10 trang 71 Tập 2

• Giải Toán 10 trang 73 Tập 2