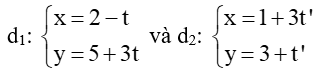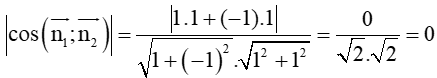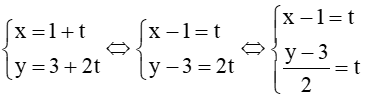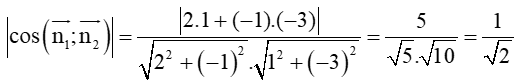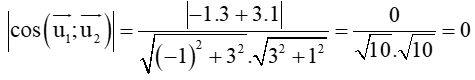Giải Toán 10 trang 73 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 73 Tập 2 trong Bài 4: Ba đường conic trong mặt phẳng toạ độ Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 73.

Giải Toán 10 trang 73 Tập 2 Chân trời sáng tạo

Thử thách trang 73 Toán lớp 10 Tập 2: Áp dụng tính chất quang học của parabol để giải quyết vấn đề sau đây:

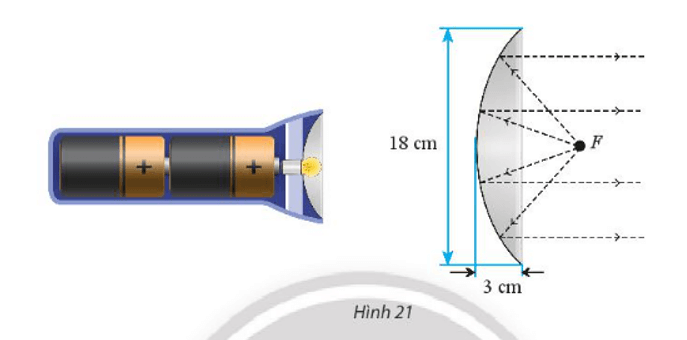
Một chóa đèn pin có mặt cắt hình parabol với kích thước như trong Hình 21.

a) Chọn hệ chục tọa độ Oxy sao cho gốc O là đỉnh của parabol và trục Ox đi qua tiêu điểm. Viết phương trình của parabol trong hệ tọa độ vừa chọn.

b) Để đèn chiếu được xa phải đặt bóng đèn cách đỉnh của chóa đèn bao nhiêu xentimét?

Lời giải:

Đặt hệ trục tọa độ như hình vẽ:

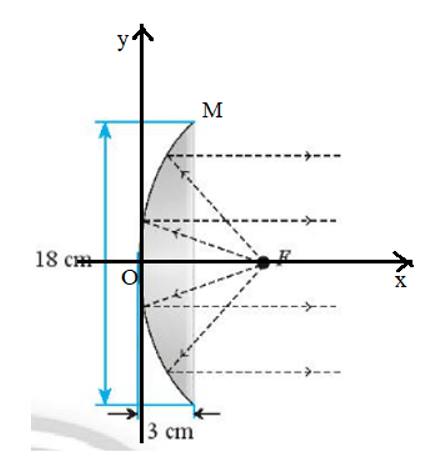
Phương trình parabol cần tìm có dạng y² = 2px.

Điểm M(3; 9) thuộc parabol trên nên ta có:

9² = 2p.3

⇔ 6p = 81

⇔ p = $\frac{81}{6}$

Suy ra phương trình parabol là y² = 2.$\frac{81}{6}$.x ⇔ y² = $\frac{81}{3}$x.

Vậy phương trình parabol cần tìm là y² = $\frac{81}{3}$x.

b) Để đèn chiếu được xa thì phải đặt bóng đèn tại tiêu điểm F của parabol.

Ta có: F = $\left(\frac{p}{2};0\right)=\left(\frac{\frac{81}{6}}{2};0\right)=\left(\frac{81}{12};0\right)$.

Vậy để đèn chiếu được xa thì phải đặt bóng đèn cách đỉnh của chóa đèn $\frac{81}{12}$ xentimét.

Bài 1 trang 73 Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho bốn điểm A(2; 1), B(1; 4), C(4; 5), D(5; 2).

a) Chứng minh ABCD là một hình vuông.

b) Tìm tọa độ tâm I của hình vuông ABCD.

Lời giải:

Ta có: $\overrightarrow{AB}$ = (-1; 3) ⇒ AB = $\sqrt{{(-1)}^2+3^2}=\sqrt{10}$

$\overrightarrow{DC}$ = (-1; 3) ⇒ DC = $\sqrt{{(-1)}^2+3^2}=\sqrt{10}$

⇒ $\overrightarrow{AB}=\overrightarrow{DC}$ ⇒ AB // CD và AB = DC

⇒ ABCD là hình bình hành (1)

Ta lại có: $\overrightarrow{AD}$ = (3; 1)

⇒ $\overrightarrow{AB}.\overrightarrow{AD}$ = (-1).3 + 3.1 = 0

⇒ $\overrightarrow{AB}\perp \overrightarrow{AD}$

⇒ $\widehat{BAD}=90°$ (2)

Từ (1) và (2) suy ra ABCD là hình vuông.

b) Vì I là tâm của hình vuông ABCD nên I là giao điểm của hai đường cheoc AC và BD hay I là trung điểm của AC. Khi đó tọa độ điểm I là:

⇒ I(3; 3).

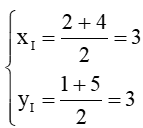
Vậy tọa độ tâm I của hình vuông ABCD là I(3; 3).

Bài 2 trang 73 Toán lớp 10 Tập 2: Cho AB và CD là hai dây cung vuông góc tại E của đường tròn (O). Vẽ hình chữ nhật AECF. Dùng phương pháp tọa độ để chứng minh EF vuông góc với DB.

Lời giải:

Ta có hình vẽ sau:

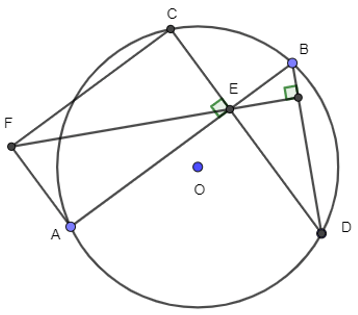
Đặt AE = a, EB = b, EC = c, ED = d.

Ta chọn hệ trục tọa độ sao cho E(0; 0), A(a; 0), B(b; 0), C(0; c) và D(0; d) và F(a; c).

Xét ∆AEC và ∆DEB, có:

$\widehat{AEC}=\widehat{DEB}=90°$

$\widehat{CAE}=\widehat{BDE}$ (hai góc nội tiếp cùng chắn $\stackrel{⏜}{CB}$)

⇒ ∆AEC ∽ ∆DEB (g – g)

⇒ $\frac{AE}{DE}=\frac{AC}{DB}=\frac{EC}{EB}$

⇒ $\frac{AE}{DE}=\frac{EC}{EB}$

⇔ AE.EB = DE.EC

⇔ AE.EB = DE.EC

⇔ a.b = d.c

⇔ d.c – ab = 0

Ta có: $\overrightarrow{\text{EF}}$ = (a; c), $\overrightarrow{BD}$ = (-b; d)

⇒ $\overrightarrow{\text{EF}}.\overrightarrow{BD}$ = a.(-b) + c.d = - ab + cd = 0

⇒ $\overrightarrow{\text{EF}}\perp \overrightarrow{BD}$

⇒ EF ⊥ BD.

Bài 3 trang 73 Toán lớp 10 Tập 2: Tìm tọa độ giao điểm và góc giữa hai đường thẳng d₁ và d₂ trong mỗi trường hợp sau:

a) d₁: x – y + 2 = 0 và d₂: x + y + 4 = 0;

b) d₁: 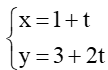và d₂: x – 3y + 2 = 0;

c)

Lời giải:

a) Gọi A là giao điểm của đường thẳng d₁ và d₂. Khi đó tọa độ điểm A là nghiệm của hệ phương trình:

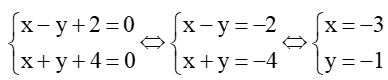
⇒ A(-3; -1).

Ta có:

Đường thẳng d₁: x – y + 2 = 0 có VTPT là $\overrightarrow{n_1}$(1; -1);

Đường thẳng d₂: x + y + 4 = 0 có VTPT là $\overrightarrow{n_2}$(1; 1);

Áp dụng công thức tính góc giữa hai đường thẳng ta có:

cos(d₁; d₂) =

⇒ (d₁; d₂) = 90°

Vậy giao điểm của hai đường thẳng d₁ và d₂ là A(-3; -1) và góc giữa hai đường thẳng d₁ và d₂ là 90°.

b) Ta có: d₁:

⇔ x – 1 = $\frac{y-3}{2}$

⇔ 2x – 2 = y – 3

⇔ 2x – y + 1 = 0

Gọi B là giao điểm của đường thẳng d₁ và d₂. Khi đó tọa độ điểm B là nghiệm của hệ phương trình:

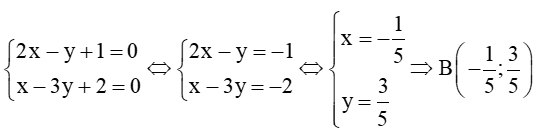
Ta có:

Đường thẳng d₁: 2x – y + 1 = 0 có VTPT là $\overrightarrow{n_1}$(2; -1);

Đường thẳng d₂: x – 3y + 2 = 0 có VTPT là $\overrightarrow{n_2}$(1; -3);

Áp dụng công thức tính góc giữa hai đường thẳng ta có:

cos(d₁; d₂) =

⇒ (d₁; d₂) = 45°

Vậy giao điểm của hai đường thẳng d₁ và d₂ là $B\left(-\frac{1}{5};\frac{3}{5}\right)$ và góc giữa hai đường thẳng d₁ và d₂ là 45°.

c) Gọi C là giao điểm của đường thẳng d₁ và d₂. Khi đó tọa độ điểm C là nghiệm của hệ phương trình:

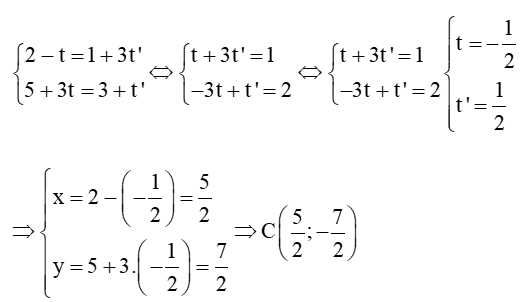
Ta có:

Đường thẳng d₁: 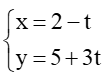có VTCP là $\overrightarrow{u_1}$ = (-1; 3);

Đường thẳng d₂: 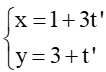có VTCP là $\overrightarrow{u_2}$ = (3; 1).

Áp dụng công thức tính góc giữa hai đường thẳng ta có:

cos(d₁; d₂) =

⇒ (d₁; d₂) = 90°

Vậy giao điểm của hai đường thẳng d₁ và d₂ là $C\left(\frac{5}{2};\frac{7}{2}\right)$ và góc giữa hai đường thẳng d₁ và d₂ bằng 90°.

Lời giải bài tập Toán lớp 10 Bài 4: Ba đường conic trong mặt phẳng toạ độ Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 63 Tập 2

• Giải Toán 10 trang 64 Tập 2

• Giải Toán 10 trang 65 Tập 2

• Giải Toán 10 trang 66 Tập 2

• Giải Toán 10 trang 67 Tập 2

• Giải Toán 10 trang 68 Tập 2

• Giải Toán 10 trang 70 Tập 2

• Giải Toán 10 trang 71 Tập 2