Giải Toán 10 trang 71 Tập 2 Chân trời sáng tạo
Haylamdo biên soạn và sưu tầm giải Toán 10 trang 71 Tập 2 trong Bài 4: Ba đường conic trong mặt phẳng toạ độ Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 71.
Giải Toán 10 trang 71 Tập 2 Chân trời sáng tạo
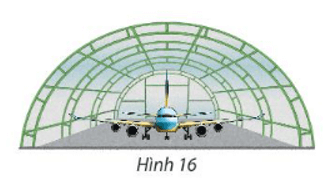
Bài 4 trang 71 Toán lớp 10 Tập 2: Một nhà vòm chứa máy bay có mặt cắt hình nửa elip cao 8m, rộng 20m (Hình 16).
a) Chọn hệ tọa độ thích hợp và viết phương trình của elip nói trên.
b) Tính khoảng cách theo phương thẳng đứng từ một điểm cách chân tường 5m lên nóc nhà vòm
Lời giải:
Đặt hệ trục tọa độ như sau:
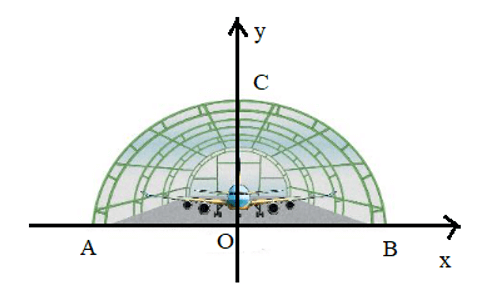
Theo hình vẽ ta thấy AB là độ dài trục lớn của elip và cũng chính là chiều rộng của nhà vòm nên 2a = 20 ⇔ a = 10.
OC là một nửa trục bé hay chính là chiều cao của nhà vòm nên b = 8.
Khi đó phương trình của elip trên là:
⇔ (*)
Vậy phương trình elip đã cho là .
b) Gọi điểm D là điểm nằm trên elip và cách chân tường 5m.
Khi đó khoảng cách từ D đến gốc tọa độ O là 10 – 5 = 5m. Hay chính là hoành độ của điểm D.
Gọi D(5; yD)
Vi D thuộc elip trên nên tọa độ điểm D thỏa mãn phương trình (*), ta có:
⇔
⇔
⇔ yD =
⇒ D(5; )
Suy ra khoảng cách theo phương thẳng đứng từ một điểm cách chân tường 5m đến nóc nhà là tung độ của điểm D là (m).
Vậy khoảng cách theo phương thẳng đứng từ một điểm cách chân tường 5m đến nóc nhà là m.
Bài 5 trang 71 Toán lớp 10 Tập 2: Một tháp làm nguội của một nhà máy có mặt cắt là hình hypebol có phương trình (Hình 17). Biết chiều cao của tháp là 150m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng khoảng cách từ tâm đối xứng đến đáy. Tính bán kính nóc và bán kính đáy của tháp.

Lời giải:
Đặt hệ trục tọa độ như hình vẽ, điểm O là tâm đối xứng của hypebol:
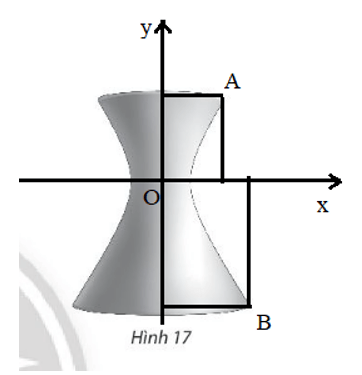
Gọi hai điểm A và B như hình vẽ.
Đặt khoảng cách từ tâm đối xứng đến đáy là h. Khi đó khoảng cách từ nóc tháp đến tâm đối xứng là h.
Theo đầu bài ta có: h + h = 150
⇔ h = 150
⇔ h = 150 :
⇔ h = 90.
Ta có khoảng cách từ nóc tháp đến tâm đối xứng của hypebol cũng chính là khoảng cách từ điểm A đến trục hoành hay là tung độ của điểm A.
⇒ yA = h = .90 = 60.
Vì A thuộc hypebol nên tọa độ điểm A thỏa mãn phương trình
⇒
⇔
⇔
⇔
⇔
⇔
⇒
Mặt khác điểm A thuộc đường tròn nóc nên khoảng cách từ A đến tâm đường tròn là bán kính của đường tròn và bằng .
Ta có khoảng cách từ nóc tháp đến tâm đối xứng của hypebol cũng chính là khoảng cách từ điểm B đến trục hoành hay là tung độ của điểm B.
⇒ yB = -h = -90.
Vì B thuộc hypebol nên tọa độ điểm B thỏa mãn phương trình
⇒
⇔
⇔
⇔
⇔
⇔
⇒
Mặt khác điểm B thuộc đường tròn nóc nên khoảng cách từ B đến tâm đường tròn là bán kính của đường tròn và bằng .
Vậy bán kính đường tròn nóc là và bán kính đường tròn đáy là .
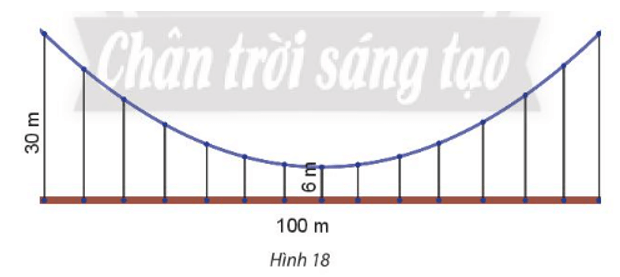
Bài 6 trang 71 Toán lớp 10 Tập 2: Một cái cầu có dây cáp treo hình parabol, cầu dài 100m và được nâng đỡ bởi những thanh thẳng đứng treo từ cáp xuống, thanh dài nhất là 30m, thanh ngắn nhất là 6m (Hình 18). Tính chiều dài của thanh cách điểm giữa cầu 18m.
Lời giải:
Ta chọn hệ tọa độ sao cho parabol có phương trình: y2 = 2px.
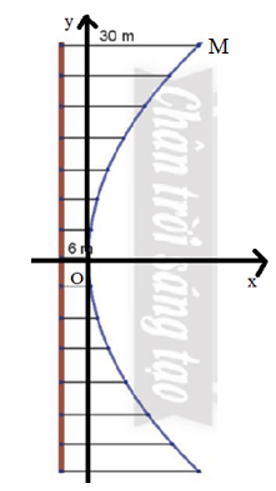
Thay điểm M(24; 50) vào phương trình trên ta được:
502 = 2p.24
⇔ p =
Khi đó phương trình parabol là: y2 = x
Gọi N là điểm nằm trên parabol cách điểm giữa cầu 18m, nghĩa là N(xN; 18).
Thay tọa độ điểm N vào parabol ta được:
182 = xN
⇔ xN =
Vậy chiều dài của thanh cách điểm giữa cầu 18m là: 3,11 + 6 = 9,11 m.
Lời giải bài tập Toán lớp 10 Bài 4: Ba đường conic trong mặt phẳng toạ độ Chân trời sáng tạo hay khác:

