Giải Toán 10 trang 97 Tập 1 Chân trời sáng tạo

❮ Bài trước Bài sau ❯

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 97 Tập 1 trong Bài 3: Tích của một số với một vectơ Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 97.

Giải Toán 10 trang 97 Tập 1 Chân trời sáng tạo

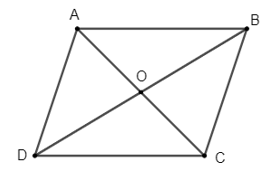
Bài 1 trang 97 Toán lớp 10 Tập 1: Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng:

a) $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M O}$ ;

b) $\vec{A B} + \vec{A C} + \vec{A D} = 2 \vec{A C}$ .

Lời giải:

Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Với M là điểm tùy ý

a) O là giao điểm hai đường chéo của hình bình hành ABCD nên O là trung điểm của AC và BD.

Khi đó: $\vec{O A} + \vec{O C} = \vec{0}, \vec{O B} + \vec{O D} = \vec{0}$

Theo quy tắc ba điểm, ta có: $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D}$

$= (\vec{M O} + \vec{O A}) + (\vec{M O} + \vec{O B}) + (\vec{M O} + \vec{O C}) + (\vec{M O} + \vec{O D})$

$= 4 \vec{M O} + (\vec{O A} + \vec{O C}) + (\vec{O B} + \vec{O D})$

$= 4 \vec{M O} + \vec{0} + \vec{0} = 4 \vec{M O}$

Vậy $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M O}$ .

b) ABCD là hình bình hành nên theo quy tắc hình bình hành ta có: $\vec{A B} + \vec{A D} = \vec{A C}$ .

Khi đó ta có: $\vec{A B} + \vec{A C} + \vec{A D} = (\vec{A B} + \vec{A D}) + \vec{A C} = \vec{A C} + \vec{A C} = 2 \vec{A C}$ .

Vậy $\vec{A B} + \vec{A C} + \vec{A D} = 2 \vec{A C}$ .

Bài 2 trang 97 Toán lớp 10 Tập 1: Cho tứ giác ABCD. Gọi M và N lần lượt là trung điểm của các cạnh AB và CD. Chứng minh rằng:

a) $\vec{A C} + \vec{B D} = 2 \vec{M N}$ ;

b) $\vec{A C} + \vec{B D} = \vec{B C} + \vec{A D}$ .

Lời giải:

a) Do M là trung điểm của AB nên $\vec{M A} + \vec{M B} = \vec{0}$ .

Do N là trung điểm của CD nên $\vec{N C} + \vec{N D} = \vec{0}$

Theo quy tắc ba điểm ta có: $\vec{A C} + \vec{B D} = (\vec{M C} - \vec{M A}) + (\vec{M D} - \vec{M B})$

$= (\vec{M C} + \vec{M D}) - (\vec{M A} + \vec{M B}) = (\vec{M C} + \vec{M D}) - (\vec{M A} + \vec{M B})$

$\vec{B C} + \vec{A D} = 2 \vec{M N} = 2 \vec{M N} + (\vec{N C} + \vec{N D}) = 2 \vec{M N} + \vec{0} = 2 \vec{M N}$

Vậy $\vec{A C} + \vec{B D} = 2 \vec{M N}$ .

b) Ta có: $\vec{B C} + \vec{A D} = (\vec{B N} + \vec{N C}) + (\vec{A N} + \vec{N D}) = (\vec{B N} + \vec{A N}) + (\vec{N C} + \vec{N D})$

$= (\vec{B N} + \vec{A N}) + \vec{0} = \vec{B N} + \vec{A N} = (\vec{M N} - \vec{M B}) + (\vec{M N} - \vec{M A})$

$= 2 \vec{M N} - (\vec{M A} + \vec{M B}) = 2 \vec{M N} - \vec{0} = 2 \vec{M N}$

Do đó: $\vec{B C} + \vec{A D} = 2 \vec{M N}$

Mà theo câu a, ta có: $\vec{A C} + \vec{B D} = 2 \vec{M N}$

Vậy $\vec{A C} + \vec{B D} = \vec{B C} + \vec{A D}$ .

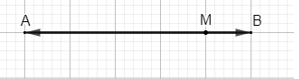
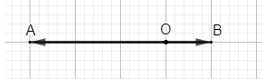
Bài 3 trang 97 Toán lớp 10 Tập 1: Cho hai điểm phân biệt A và B. Xác định điểm M sao cho $\vec{M A} + 4 \vec{M B} = \vec{0}$ .

Lời giải:

Ta có: $\vec{M A} + 4 \vec{M B} = \vec{0} \Leftrightarrow \vec{M A} = - 4 \vec{M B}$ .

Suy ra ba điểm M, A, B thẳng hàng và hai vectơ $\vec{M A}$ và $\vec{M B}$ ngược hướng và thỏa mãn $|\vec{M A}| = 4. |\vec{M B}|$ hay MA = 4MB.

Khi đó M, A, B thẳng hàng và M nằm giữa A và B thỏa mãn MA = 4MB.

Cho hai điểm phân biệt A và B. Xác định điểm M sao cho: vectơ MA + 4 vectơ MB = vectơ 0

Vậy điểm M thỏa mãn $\vec{M A} + 4 \vec{M B} = \vec{0}$ là điểm thuộc đoạn thẳng AB sao cho MA = 4MB.

Bài 4 trang 97 Toán lớp 10 Tập 1: Cho tứ giác ABCD. Gọi E, F, G lần lượt là trung điểm của các đoạn thẳng AB, CD, EF. Lấy điểm M tùy ý, chứng minh rằng $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M G}$ .

Lời giải:

Vì E là trung điểm của AB nên với điểm G ta có: $\vec{G A} + \vec{G B} = 2 \vec{G E}$ .

Vì F là trung điểm của CD nên với điểm G ta có: $\vec{G C} + \vec{G D} = 2 \vec{G F}$ .

Mà G là trung điểm của EF nên $\vec{G E} + \vec{G F} = \vec{0}$ .

Do đó: $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = 2 \vec{G E} + 2 \vec{G F} = 2 (\vec{G E} + \vec{G F}) = \vec{0}$ .

Với điểm M tùy ý, ta có: $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D}$

$= (\vec{M G} + \vec{G A}) + (\vec{M G} + \vec{G B}) + (\vec{M G} + \vec{G C}) + (\vec{M G} + \vec{G D})$

$= 4 \vec{M G} + (\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D})$

$= 4 \vec{M G} + \vec{0} = 4 \vec{M G}$

Vậy $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M G}$ .

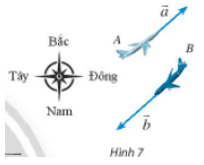
Bài 5 trang 97 Toán lớp 10 Tập 1: Máy bay A đang bay về hướng đông bắc với tốc độ 600 km/h. Cùng lúc đó, máy bay B đang bay về hướng tây nam với tốc độ 800 km/h. Biểu diễn vectơ vận tốc $\vec{b}$ của máy bay B theo vectơ vận tốc $\vec{a}$ của máy bay A.

Máy bay A đang bay về hướng đông bắc với tốc độ 600 km/h

Lời giải:

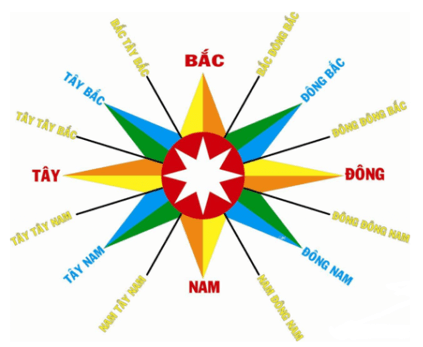
Quan sát bản đồ về hướng sau:

Máy bay A đang bay về hướng đông bắc với tốc độ 600 km/h

Ta thấy hướng đông bắc ngược hướng với hướng tây nam.

Do đó vectơ vận tốc $\vec{b}$ của máy bay B ngược hướng với vectơ vận tốc $\vec{a}$ của máy bay A. (1)

Theo bài ra ta có: $|\vec{a}| = 600$ km/h, $|\vec{b}| = 800$ km/h.

Suy ra: $\frac{|\vec{b}|}{|\vec{a}|} = \frac{800}{600} = \frac{4}{3} \Rightarrow |\vec{b}| = \frac{4}{3} . |\vec{a}|$ (2)

Từ (1) và (2) suy ra: $\vec{b} = - \frac{4}{3} \vec{a}$ .

Bài 6 trang 97 Toán lớp 10 Tập 1: Cho hai điểm phân biệt A và B.

a) Xác định điểm O sao cho $\vec{O A} + 3 \vec{O B} = \vec{0}$ .

b) Chứng minh rằng với mọi điểm M, ta có $\vec{M A} + 3 \vec{M B} = 4 \vec{M O}$ .

Lời giải:

a) Ta có: $\vec{O A} + 3 \vec{O B} = \vec{0} \Leftrightarrow \vec{O A} = - 3 \vec{O B}$

Do đó ba điểm A, O, B thẳng hàng và hai vectơ $\vec{O A}$ và $\vec{O B}$ ngược hướng thỏa mãn $|\vec{O A}| = 3. |\vec{O B}|$ .

Khi đó O nằm trên đoạn thẳng AB thỏa mãn OA = 3OB.

Cho hai điểm phân biệt A và B. Xác định điểm O sao cho vectơ OA + 3 vectơ OB = vectơ 0

b) Với điểm M bất kì ta có: $\vec{M A} + 3 \vec{M B} = (\vec{M O} + \vec{O A}) + 3 (\vec{M O} + \vec{O B})$

$= \vec{M O} + \vec{O A} + 3 \vec{M O} + 3 \vec{O B} = 4 \vec{M O} + (\vec{O A} + 3 \vec{O B}) = 4 \vec{M O} + \vec{0} = 4 \vec{M O}$

Vậy với mọi điểm M bất kì ta có $\vec{M A} + 3 \vec{M B} = 4 \vec{M O}$ .

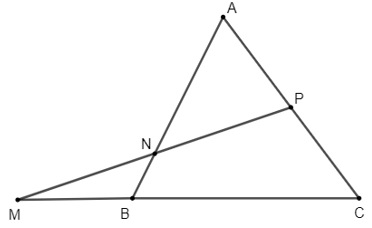
Bài 7 trang 97 Toán lớp 10 Tập 1: Cho tam giác ABC.

a) Xác định các điểm M, N, P thỏa mãn: $\vec{M B} = \frac{1}{2} \vec{B C}, \vec{A N} = 3 \vec{N B}, \vec{C P} = \vec{P A}$ .

b) Biểu thị mỗi vectơ $\vec{M N}, \vec{M P}$ theo hai vectơ $\vec{B C}, \vec{B A}$ .

c) Chứng minh ba điểm M, N, P thẳng hàng.

Lời giải:

a) Ta có: $\vec{M B} = \frac{1}{2} \vec{B C}$ nên ba điểm M, B, C thẳng hàng và vectơ $\vec{M B}$ cùng hướng với vectơ $\vec{B C}$ sao cho $|\vec{M B}| = \frac{1}{2} . |\vec{B C}|$ hay MB = $\frac{1}{2}$ BC.

Lại có: $\vec{A N} = 3 \vec{N B}$ nên ba điểm A, N, B thẳng hàng và vectơ $\vec{A N}$ cùng hướng với vectơ $\vec{N B}$ sao cho $|\vec{A N}| = 3 |\vec{N B}|$ hay AN = 3NB.

Có: $\vec{C P} = \vec{P A} \Leftrightarrow \vec{P A} - \vec{C P} = \vec{0} \Leftrightarrow \vec{P A} + (- \vec{C P}) = \vec{0} \Leftrightarrow \vec{P A} + \vec{P C} = \vec{0}$

⇔ P là trung điểm của đoạn thẳng AC.

Cho tam giác ABC. Xác định các điểm M, N, P thỏa mãn: vectơ MB = 1/2 vectơ BC, vectơ AN = 3 vectơ NB

b) Vì AN = 3NB nên BN = $\frac{1}{4}$ BA, do đó: $\vec{B N} = \frac{1}{4} \vec{B A}$ .

Ta có: $\vec{M N} = \vec{M B} + \vec{B N} = \frac{1}{2} \vec{B C} + \frac{1}{4} \vec{B A}$ .

Vì MB = $\frac{1}{2}$ BC nên $M C = \frac{3}{2} B C$ , do đó: $\vec{M C} = \frac{3}{2} \vec{B C}$ .

P là trung điểm của AC nên $\vec{C P} = \frac{1}{2} \vec{C A}$ .

Nên ta có: $\vec{M P} = \vec{M C} + \vec{C P} = \frac{3}{2} \vec{B C} + \frac{1}{2} \vec{C A} = \frac{3}{2} \vec{B C} + \frac{1}{2} (\vec{B A} - \vec{B C})$

$= (\frac{3}{2} - \frac{1}{2}) \vec{B C} + \frac{1}{2} \vec{B A} = \vec{B C} + \frac{1}{2} \vec{B A}$

Vậy $\vec{M N} = \frac{1}{2} \vec{B C} + \frac{1}{4} \vec{B A}$ và $\vec{M P} = \vec{B C} + \frac{1}{2} \vec{B A}$ .

c) Theo câu b ta có: $\vec{M N} = \frac{1}{2} \vec{B C} + \frac{1}{4} \vec{B A} = \frac{1}{2} (\vec{B C} + \frac{1}{2} \vec{B A}) = \frac{1}{2} \vec{M P}$

Do đó: $\vec{M N} = \frac{1}{2} \vec{M P}$

Từ đó suy ra ba điểm M, N, P thẳng hàng.

Lời giải bài tập Toán lớp 10 Bài 3: Tích của một số với một vectơ Chân trời sáng tạo hay khác:

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯