Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi.
Câu hỏi:
Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao AB = 70 m, phương nhìn AC tạo với phương nằm ngang góc 30°, phương nhìn BC tạo với phương nằm ngang góc 15°30' (hình vẽ).
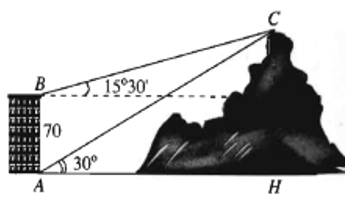
Ngọn núi đó có độ cao CH so với mặt đất gần nhất với giá trị nào sau đây?
A. 135 m;
B. 234 m;
C. 165 m;
D. 195 m.
Trả lời:
Hướng dẫn giải
Đáp án đúng là: A
Từ hình vẽ ta có
Xét tam giác ABC có ta có:
(định lí tổng ba góc trong tam giác)
Áp dụng định lí sin trong tam giác ABC, ta có:
Tam giác ACH vuông tại H nên ta có:
Vậy ngọn núi cao khoảng 135 m.
Xem thêm bài tập trắc nghiệm Toán 10 CTST có lời giải hay khác:
Câu 1:
Cho tam giác ABC, biết BC = 24, AC = 13, AB = 15. Số đo góc A là:
Xem lời giải »
Câu 2:
Tam giác ABC có AB = 117. Độ dài cạnh AC là khoảng:
Xem lời giải »
Câu 3:
Tam giác ABC có và . Độ dài cạnh BC là:
Xem lời giải »
Câu 4:
Cho tam giác ABC có BC = 2. Số đo của là:
Xem lời giải »
Câu 5:
Trong sơ đồ, chùm sáng S hướng vào gương màu xanh, phản xạ vào gương màu đỏ và sau đó phản xạ vào gương màu xanh như hình vẽ. Biết OP = 2 m, m.
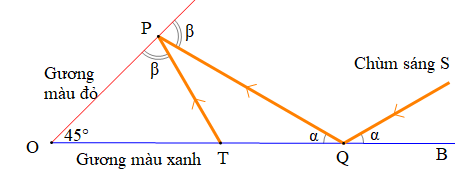
Khi đó đoạn PT bằng:
Xem lời giải »



