Từ hai vị trí A và B của một tòa nhà, người ta quan sát được đỉnh C của ngọn núi. Biết rằng độ cao của tòa nhà là AB = 70 m, phương nhìn AC tạo với phương ngang AH một góc bằng 30°, phương nh
Câu hỏi:
Từ hai vị trí A và B của một tòa nhà, người ta quan sát được đỉnh C của ngọn núi. Biết rằng độ cao của tòa nhà là AB = 70 m, phương nhìn AC tạo với phương ngang AH một góc bằng 30°, phương nhìn BC tạo với phương ngang BD một góc bằng 15°30’.
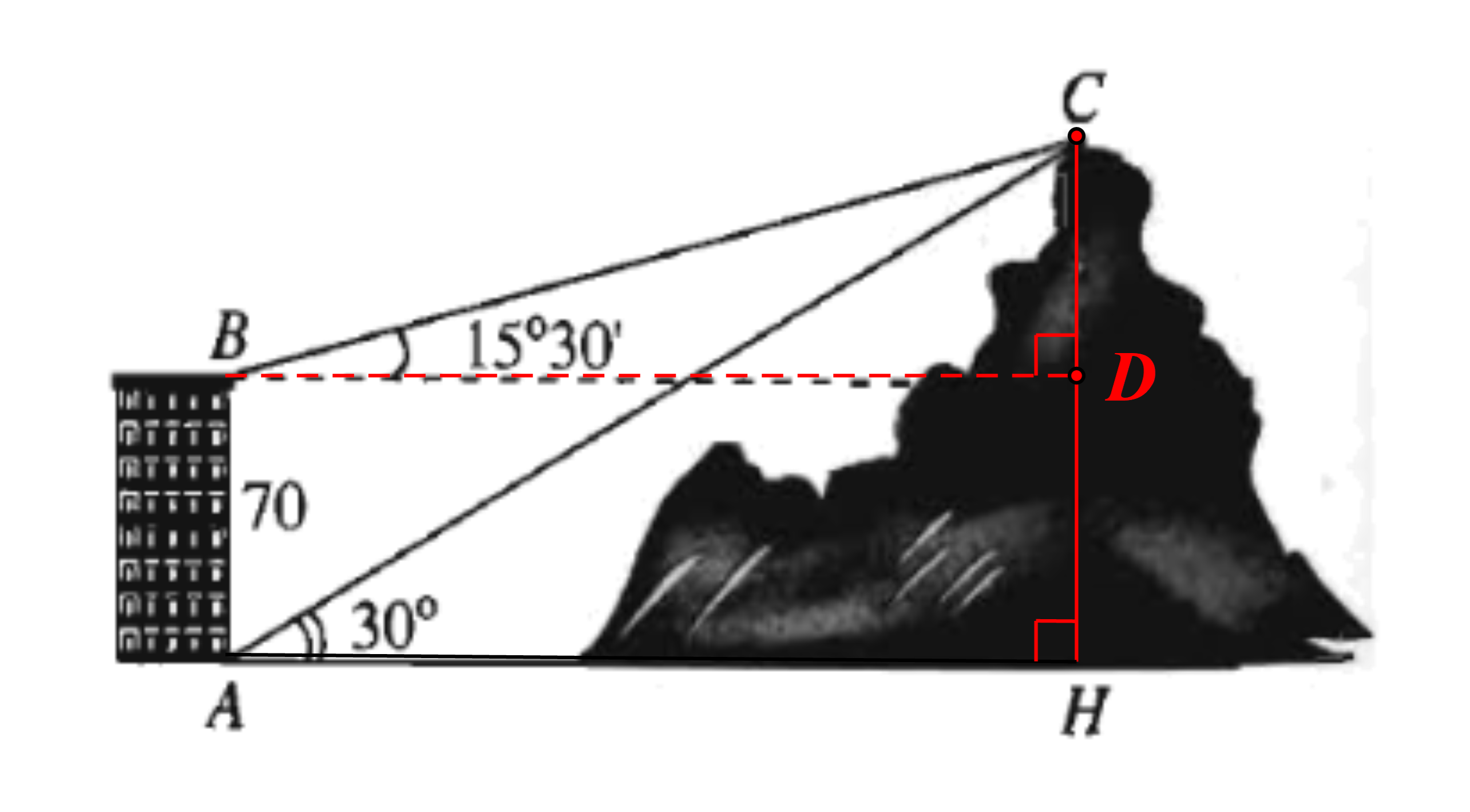
Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây?
Trả lời:
Hướng dẫn giải
Đáp án đúng là: A
Ta có \(\widehat {BAC} + \widehat {CAH} = \widehat {BAH} = 90^\circ \).
\[ \Rightarrow \widehat {BAC} = 90^\circ - 30^\circ = 60^\circ \].
Ta có \(\widehat {ABC} = \widehat {ABD} + \widehat {DBC} = 90^\circ + 15^\circ 30' = 105^\circ 30'\).
∆ABC có \(\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \) (định lí tổng ba góc trong một tam giác)
Suy ra \(\widehat {ACB} = 180^\circ - \left( {\widehat {BAC} + \widehat {ABC}} \right) = 180^\circ - \left( {60^\circ + 105^\circ 30'} \right) = 14^\circ 30'\).
Áp dụng định lí sin cho ∆ABC, ta được \(\frac{{AC}}{{\sin \widehat {ABC}}} = \frac{{AB}}{{\sin \widehat {ACB}}}\)
Suy ra \(AC = \frac{{AB.\sin \widehat {ABC}}}{{\sin \widehat {ACB}}} = \frac{{70.\sin 105^\circ 30'}}{{\sin 14^\circ 30'}} \approx 269,4\) (m)
∆ACH vuông tại H: \(\sin \widehat {CAH} = \frac{{CH}}{{AC}}\)
Suy ra \(CH = AC.\sin \widehat {CAH} \approx 269,4.\sin 30^\circ = 134,7\) (m)
Vậy ngọn núi cao khoảng 134,7 m.
Giá trị này gần với 135 m nhất.
Do đó ta chọn phương án A.

