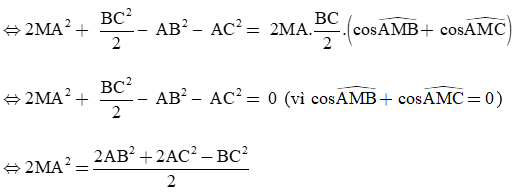Bài 3.16 trang 44 Toán 10 Tập 1 - Kết nối tri thức

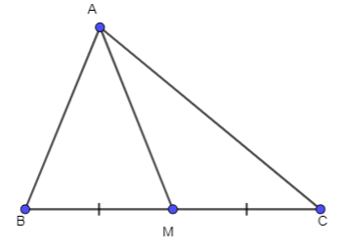
Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:

Giải Toán lớp 10 Bài tập cuối chương III

Bài 3.16 trang 44 Toán 10 Tập 1: Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:

a) $c o s \hat{A M B} + c o s \hat{A M C} = 0;$

b) MA² + MB² – AB² = 2MA.MB.cos $\hat{A M B}$ và MA² + MC² – AC² = 2MA.MC.cos $\hat{A M C}$ ;

c) $M A^{2} = \frac{2 (A B^{2} + A C^{2}) - B C^{2}}{4}$ (công thức đường trung tuyến).

Lời giải:

Bài 3.16 trang 44 Toán 10 Tập 1 | Kết nối tri thức Giải Toán lớp 10

a) $c o s \hat{A M B} + c o s \hat{A M C} = 0$

Ta có: $\hat{A M B} + \hat{A M C} = 180^{0}$

$\hat{A M C} = 180^{0} - \hat{A M B}$

$c o s \hat{A M B} = - c o s (180^{0} - \hat{A M B}) = - c o s \hat{A M C}$

$\Rightarrow c o s \hat{A M B} + c o s \hat{A M C}$

$= - c o s \hat{A M C} + c o s \hat{A M C} = 0$

b) Xét ΔAMB, ta có:

AB² = MA² + MB² – 2MA.MB.cos $\hat{A M B}$

⇔ MA² + MB² – AB² = 2MA.MB.cos $\hat{A M B}$ (1)

Xét ΔAMC, ta có:

AC² = MA² + MC² – 2MA.MC.cos $\hat{A M C}$

⇔ MA² + MC² – AC² = 2MA.MC.cos $\hat{A M C}$ (2)

c) Cộng vế với vế của (1) với (2), ta được:

MA² + MB² – AB² + MA² + MC² – AC² = 2MA.MB.cos $\hat{A M B}$ + 2MA.MC.cos $\hat{A M C}$

$\Leftrightarrow 2 M A^{2} + \frac{B C^{2}}{4} - A B^{2} + \frac{B C^{2}}{4} - A C^{2}$

$= 2 M A . \frac{B C}{2} . c o s \hat{A M B} + 2 M A . \frac{B C}{2} . c o s \hat{A M C}$

(Vì $M B = M C = \frac{B C}{2}$ )

Bài 3.16 trang 44 Toán 10 Tập 1 | Kết nối tri thức Giải Toán lớp 10

$\Leftrightarrow M A^{2} = \frac{2 (A B^{2} + A C^{2}) - B C^{2}}{4}$ (công thức đường trung tuyến).

Lời giải bài tập Toán 10 Bài tập cuối chương 3 hay, chi tiết khác:

<<<<<<< HEAD ======= >>>>>>> 7de0ce75c76253c52280308e94cf2d713ccea5e2