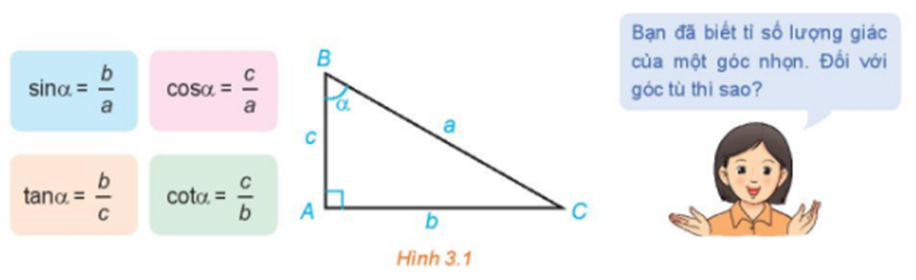
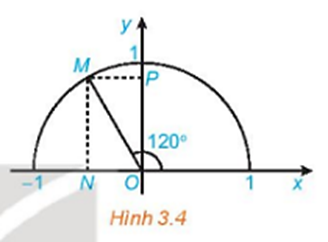
Đơn giản các biểu thức sau: a) sin1000 + sin800 + cos160 + cos 1640;
Câu hỏi:
Đơn giản các biểu thức sau:
a) sin1000 + sin800 + cos160 + cos 1640;
b) với .
Trả lời:
a) sin1000 + sin800 + cos160 + cos 1640
= sin1000 + sin1000 + cos1640 + cos1640
= 2sin1000 + 2cos1640.
b)
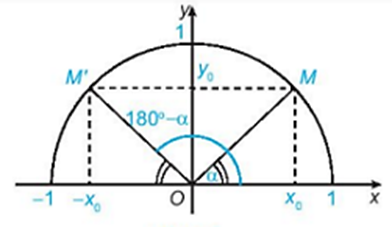
Với 0o < α < 90o, ta có:
sin (180o – α) = sin α; cos (180o – α) = – cos α;
tan (180o – α) = – tan α; cot (180o – α) = – cot α.
Khi đó,
2sin (180o – α) . cot α – cos (180o – α) . tan α . cot (180o – α)
= 2sin α . cot α – (– cos α) . tan α . (– cot α)
= 2sin α . cot α – cos α . tan α . cot α
= 2sin α . – cos α .
= 2cos α – cos α = cos α.