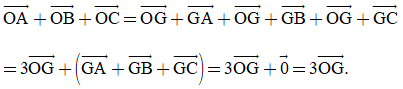Giải Toán 10 trang 57 Tập 1 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 57 Tập 1 trong Bài 9: Tích của một vectơ với một số Toán lớp 10 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 57.

Giải Toán 10 trang 57 Tập 1 Kết nối tri thức

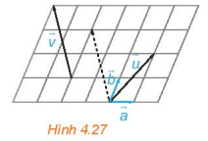
HĐ3 trang 57 Toán 10 Tập 1: Với $\overrightarrow{u}\ne \overrightarrow{0}$ và hai số thực k, t, những khẳng định nào sau đây là đúng?

a) Hai vecto $k\left(t\overrightarrow{u}\right)$ và $\left(kt\right)\overrightarrow{u}$ có cùng độ dài bằng $\left|kt\right|\left|\overrightarrow{u}\right|.$

b) Nếu kt ≥ 0 thì cả hai vecto $k\left(t\overrightarrow{u}\right),\left(kt\right)\overrightarrow{u}$cùng hướng với $\overrightarrow{u}$.

c) Nếu kt < 0 thì cả hai vecto $k\left(t\overrightarrow{u}\right),\left(kt\right)\overrightarrow{u}$ ngược hướng với $\overrightarrow{u}$.

d) Hai vecto $k\left(t\overrightarrow{u}\right)$ và $\left(kt\right)\overrightarrow{u}$ bằng nhau.

Lời giải:

a) Ta có: 

$\left|k\left(t\overrightarrow{u}\right)\right|=\left|k\right|\left|t\overrightarrow{u}\right|=\left|k\right|\left|t\right|\left|\overrightarrow{u}\right|=\left|kt\right|\left|\overrightarrow{u}\right|$

và $\left|\left(kt\right)\overrightarrow{u}\right|=\left|kt\right|\left|\overrightarrow{u}\right|$

Suy ra $\left|k\left(t\overrightarrow{u}\right)\right|=\left|\left(kt\right)\overrightarrow{u}\right|=\left|kt\right|\left|\overrightarrow{u}\right|$

Do đó hai vecto $k\left(t\overrightarrow{u}\right)$ và $\left(kt\right)\overrightarrow{u}$ có cùng độ dài bằng $\left|kt\right|\left|\overrightarrow{u}\right|.$

Vậy khẳng định a) đúng.

b) Vecto $\left(kt\right)\overrightarrow{u}$ cùng hướng với vecto $\overrightarrow{u}$ khi kt ≥ 0

Vecto $k\left(t\overrightarrow{u}\right)$ cùng hướng với vecto $t\overrightarrow{u}$ khi k ≥ 0

Vecto $t\overrightarrow{u}$ cùng hướng với vecto $\overrightarrow{u}$ khi t ≥ 0

Suy ra $k\left(t\overrightarrow{u}\right)$ cùng hướng với vecto $\overrightarrow{u}$ khi kt ≥ 0.

Do đó nếu kt ≥ 0 thì cả hai vecto $k\left(t\overrightarrow{u}\right),\left(kt\right)\overrightarrow{u}$cùng hướng với $\overrightarrow{u}$.

Vậy khẳng định b) là đúng.

c) Vecto $\left(kt\right)\overrightarrow{u}$ ngược hướng với vecto $\overrightarrow{u}$ khi kt < 0

Vecto $k\left(t\overrightarrow{u}\right)$ ngược hướng với vecto $t\overrightarrow{u}$ khi k < 0

Vecto $t\overrightarrow{u}$ ngược hướng với vecto $\overrightarrow{u}$ khi t < 0

Suy ra $k\left(t\overrightarrow{u}\right)$ ngược hướng với vecto $\overrightarrow{u}$ khi kt < 0.

Do đó nếu kt < 0 thì cả hai vecto $k\left(t\overrightarrow{u}\right),\left(kt\right)\overrightarrow{u}$ ngược hướng với $\overrightarrow{u}$.

Vậy khẳng định c) là đúng.

d) Hai vecto $k\left(t\overrightarrow{u}\right)$ và $\left(kt\right)\overrightarrow{u}$ có cùng độ dài (theo ý a)

Nếu kt ≥ 0 thì cả hai vecto $k\left(t\overrightarrow{u}\right),\left(kt\right)\overrightarrow{u}$ cùng hướng với $\overrightarrow{u}$.

Suy ra hai vecto $k\left(t\overrightarrow{u}\right),\left(kt\right)\overrightarrow{u}$ cùng hướng .

Nếu kt < 0 thì cả hai vecto $k\left(t\overrightarrow{u}\right),\left(kt\right)\overrightarrow{u}$ ngược hướng với $\overrightarrow{u}$.

Suy ra hai vecto $k\left(t\overrightarrow{u}\right),\left(kt\right)\overrightarrow{u}$ cùng hướng.

Do đó hai vecto $k\left(t\overrightarrow{u}\right),\left(kt\right)\overrightarrow{u}$ cùng hướng với mọi k, t.

$\Rightarrow k\left(t\overrightarrow{u}\right)=\left(kt\right)\overrightarrow{u}$

Vậy khẳng định d) đúng.

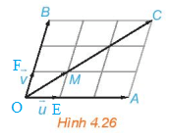
HĐ4 trang 57 Toán 10 Tập 1: Hãy chỉ ra trên Hình 4.25 hai vecto $3\left(\overrightarrow{u}+\overrightarrow{v}\right)$ và $3\overrightarrow{u}+3\overrightarrow{v}$. Từ đó, nêu mối quan hệ giữa $3\left(\overrightarrow{u}+\overrightarrow{v}\right)$ và $3\overrightarrow{u}+3\overrightarrow{v}$.

Lời giải:

Xét hình bình hành OEMF, ta có:

$\overrightarrow{u}+\overrightarrow{v}=\overrightarrow{OE}+\overrightarrow{\text{OF}}=\overrightarrow{OM}$ (quy tắc hình bình hành)

$\Rightarrow 3\left(\overrightarrow{u}+\overrightarrow{v}\right)=3\overrightarrow{OM}=\overrightarrow{OC}$

Xét hình bình hành OACB, ta có:

$3\overrightarrow{u}+3\overrightarrow{v}=\overrightarrow{OA}+\overrightarrow{\text{OB}}=\overrightarrow{OC}$ (quy tắc hình bình hành)

$\Rightarrow 3\left(\overrightarrow{u}+\overrightarrow{v}\right)=3\overrightarrow{u}+3\overrightarrow{v}\left(=\overrightarrow{OC}\right)$

Vậy $3\left(\overrightarrow{u}+\overrightarrow{v}\right)=3\overrightarrow{u}+3\overrightarrow{v}.$

Luyện tập 2 trang 57 Toán 10 Tập 1: Cho tam giác ABC có trọng tâm G. Chứng minh với điểm O tùy ý, ta có:

$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OG}$

Lời giải:

Vì G là trọng tâm tam giác ABC nên ta có:

$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$.

Do đó:

Vậy $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OG}.$

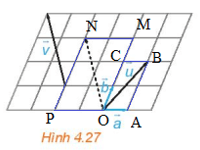
Luyện tập 3 trang 57 Toán 10 Tập 1: Trong Hình 4.27, hãy biểu thị mỗi vecto $\overrightarrow{u},\overrightarrow{v}$ theo hai vecto $\overrightarrow{a},\overrightarrow{b}$, tức là tìm các số x, y, z, t để $\overrightarrow{u}=x\overrightarrow{a}+y\overrightarrow{b},\overrightarrow{v}=t\overrightarrow{a}+z\overrightarrow{b}.$

Lời giải:

Ta có hình vẽ sau:

Xét hình bình hành OABC, có:

$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OC}=2\overrightarrow{b},\overrightarrow{OB}=\overrightarrow{u}$

Khi đó, ta có:

$\overrightarrow{u}=\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{a}+2\overrightarrow{b}$ (quy tắc hình bình hành)

Xét hình bình hành OMNP, có:

$\overrightarrow{ON}=\overrightarrow{v},\overrightarrow{OM}=3\overrightarrow{b},\overrightarrow{OP}=-2\overrightarrow{a}$

Khi đó, ta có:

$$\begin{gathered} \overrightarrow{v}=\overrightarrow{ON}=\overrightarrow{OM}+\overrightarrow{OP}=3\overrightarrow{b}-2\overrightarrow{a} \\ =-2\overrightarrow{a}+3\overrightarrow{b}. \end{gathered}$$

Vậy  $\overrightarrow{u}=\overrightarrow{a}+2\overrightarrow{b},\overrightarrow{v}=-2\overrightarrow{a}+3\overrightarrow{b}.$

Lời giải bài tập Toán lớp 10 Bài 9: Tích của một vectơ với một số Kết nối tri thức hay khác:

• Giải Toán 10 trang 55
• Giải Toán 10 trang 56
• Giải Toán 10 trang 58
• Giải Toán 10 trang 59