Bài 2 trang 115 Toán 11 Tập 2 Cánh diều

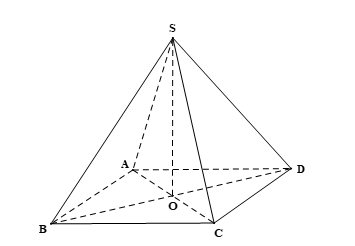
Cho hình chóp đều S.ABCD có các cạnh bên và các cạnh đáy đều bằng a.

Giải Toán 11 Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối - Cánh diều

Bài 2 trang 115 Toán 11 Tập 2: Cho hình chóp đều S.ABCD có các cạnh bên và các cạnh đáy đều bằng a.

a) Chứng minh rằng các tam giác ASC và BSD là tam giác vuông cân.

b) Gọi O là giao điểm của AC và BD, chứng minh rằng đường thẳng SO vuông góc với mặt phẳng (ABCD).

c) Chứng minh rằng góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng 45°.

Lời giải:

Bài 2 trang 115 Toán 11 Tập 2 | Cánh diều Giải Toán 11

a) Do S.ABCD là hình chóp đều nên SA = SB = SC = SD = a.

Vì ABCD là hình vuông nên AC = BC và $\hat{A B C} = 90 ° .$

Áp dụng định lí Pythagore vào tam giác ABC vuông tại B có:

AC² = AB² + BC² = a² + a² = 2a².

Mà AC = BD nên BD² = AC² = 2a².

⦁ Xét ∆ASC có: SA² + SC² = a² + a² = 2a² = AC².

Nên theo định lí Pythagore đảo ta có tam giác ASC vuông tại S.

Mà SA = SC nên tam giác ASC vuông cân tại S.

⦁ Xét tam giác BSD có: SB² + SD² = a² + a² = 2a² = BD².

Nên theo định lí Pythagore đảo ta có tam giác BSD vuông tại S.

Mà SB = SD nên tam giác BSD vuông cân tại S.

b) Do ABCD là hình vuông và O = AC ∩ BD nên O là trung điểm của AC và BD.

Xét ∆ASC vuông cân tại S có: SO là đường trung tuyến (do O là trung điểm của AC) nên cũng đồng thời là đường cao của tam giác. Do đó SO ⊥ AC.

Xét ∆BSD vuông cân tại S có: SO là đường trung tuyến (do O là trung điểm của BD) nên cũng đồng thời là đường cao của tam giác. Do đó SO ⊥ BD.

Ta có: SO ⊥ AC, SO ⊥ BD và AC ∩ BD = O trong (ABCD).

Do đó SO ⊥ (ABCD).

c) Vì SO ⊥ (ABCD) nên OA là hình chiếu của SA trên (ABCD).

Suy ra góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng góc $\hat{S A O} .$

Lại có tam giác ASC là tam giác vuông cân tại S nên $\hat{S A O} = 45 ° .$

Vậy góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng 45°.

Lời giải bài tập Toán 11 Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối hay, chi tiết khác: