Luyện tập 2 trang 110 Toán 11 Tập 2 Cánh diều

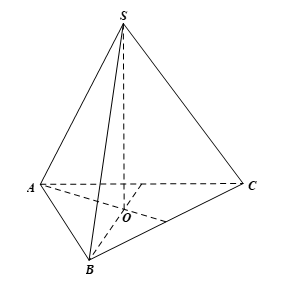
Cho hình chóp tam giác đều S.ABC. Chứng minh rằng các cạnh bên tạo với mặt phẳng chứa đáy các góc bằng nhau.

Giải Toán 11 Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối - Cánh diều

Luyện tập 2 trang 110 Toán 11 Tập 2: Cho hình chóp tam giác đều S.ABC. Chứng minh rằng các cạnh bên tạo với mặt phẳng chứa đáy các góc bằng nhau.

Lời giải:

Luyện tập 2 trang 110 Toán 11 Tập 2 | Cánh diều Giải Toán 11

Do S.ABC là hình chóp tam giác đều nên SA = SB = SC (các cạnh bên bằng nhau).

Gọi O là chân đường cao của hình chóp tam giác đều S.ABC.

Do SO ⊥ (ABC) nên SO ⊥ OA, SO ⊥ OB, SO ⊥ OC.

Xét ∆SAO và ∆SBO có:

$\hat{S O A} = \hat{S O B} = 90 °;$

SO là cạnh chung;

SA = SB (chứng minh trên)

Do đó ∆SAO = ∆SBO (cạnh huyền – cạnh góc vuông)

Suy ra $\hat{S A O} = \hat{S C O}$ (hai góc tương ứng)

Chứng minh tương tự, ta cũng có∆SAO = ∆SCO nên $\hat{S A O} = \hat{S C O} .$

Từ đó ta có: $\hat{S A O} = \hat{S B O} = \hat{S C O} .$

Vậy các cạnh bên tạo với mặt phẳng chứa đáy các góc bằng nhau.

Lời giải bài tập Toán 11 Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối hay, chi tiết khác: