Giải Toán 11 trang 82 Tập 2 Cánh diều
Haylamdo biên soạn và sưu tầm lời giải Toán 11 trang 82 Tập 2 trong Bài 2: Đường thẳng vuông góc với mặt phẳng Toán 11 Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 11 dễ dàng làm bài tập Toán 11 trang 82.
Giải Toán 11 trang 82 Tập 2 Cánh diều
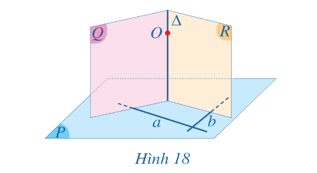
Hoạt động 4 trang 82 Toán 11 Tập 2: Cho mặt phẳng (P) và điểm O. Gọi a, b là hai đường thẳng cắt nhau thuộc mặt phẳng (P) sao cho a và b không đi qua O. Lấy hai mặt phẳng (Q), (R) lần lượt đi qua O và vuông góc a, b (Hình 18).
a) Giao tuyến ∆ của hai mặt phẳng (Q), (R) có vuông góc với mặt phẳng (P) hay không?
b) Có bao nhiêu đường thẳng đi qua O và vuông góc với (P)?
Lời giải:
a) Do a ⊥ (Q) và ∆ ⊂ (Q) nên a ⊥ ∆.
b ⊥ (R) và ∆ ⊂ (R) nên b ⊥ ∆.
Mà a, b là hai đường thẳng cắt nhau thuộc mặt phẳng (P)
Suy ra ∆ ⊥ (P).
Vậy giao tuyến ∆ của hai mặt phẳng (Q), (R) có vuông góc với mặt phẳng (P).
b) Theo câu a, ta có ∆ ⊥ (P) với ∆ là giao tuyến của hai mặt phẳng (Q), (R); với hai mặt phẳng (Q), (R) lần lượt đi qua O và vuông góc a, b.
Vì hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng. Tức là tồn tại duy nhất một đường thẳng ∆ đi qua O (điểm chung của 2 mặt phẳng (Q) và (R)).
Vậy có duy nhất một đường thẳng đi qua O và vuông góc với (P).
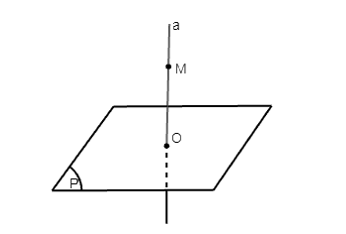
Luyện tập 3 trang 82 Toán 11 Tập 2: Cho mặt phẳng (P) và đường thẳng a cắt nhau tại điểm O, a ⊥ (P). Giả sử điểm M thỏa mãn OM ⊥ (P). Chứng minh rằng M ∈ a.
Lời giải:
Ta có a ⊥ (P) tại O.
Mặt khác, có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước, tức là tồn tại duy nhất đường thẳng a đi qua điểm O và vuông góc với mặt phẳng (P).
Nên nếu OM ⊥ (P) thì M ∈ a.
Lời giải bài tập Toán 11 Bài 2: Đường thẳng vuông góc với mặt phẳng hay khác: